接雨水

|

接雨水问题详解

接雨水这道题目挺有意思，在面试题中出现频率还挺高的，本文就来步步优化，讲解一下这道题。
先看一下题目：

就是用一个数组表示一个条形图，问你这个条形图最多能接多少水。

1
int trap(int[] height);

下面就来由浅入深介绍暴力解法 -> 备忘录解法 -> 双指针解法，在 O(N) 时间 O(1) 空间内解决这个问题。

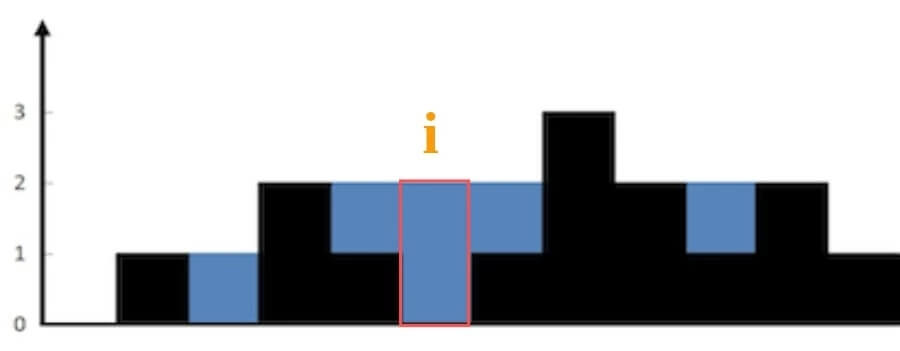
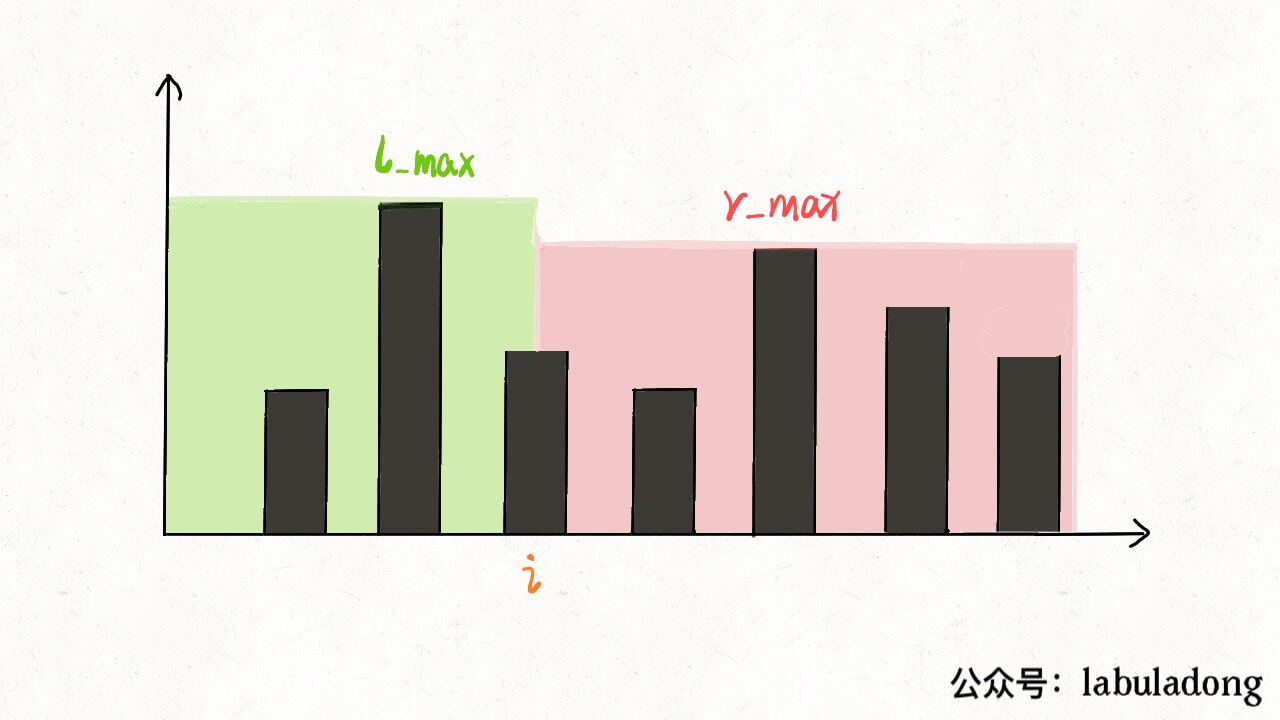
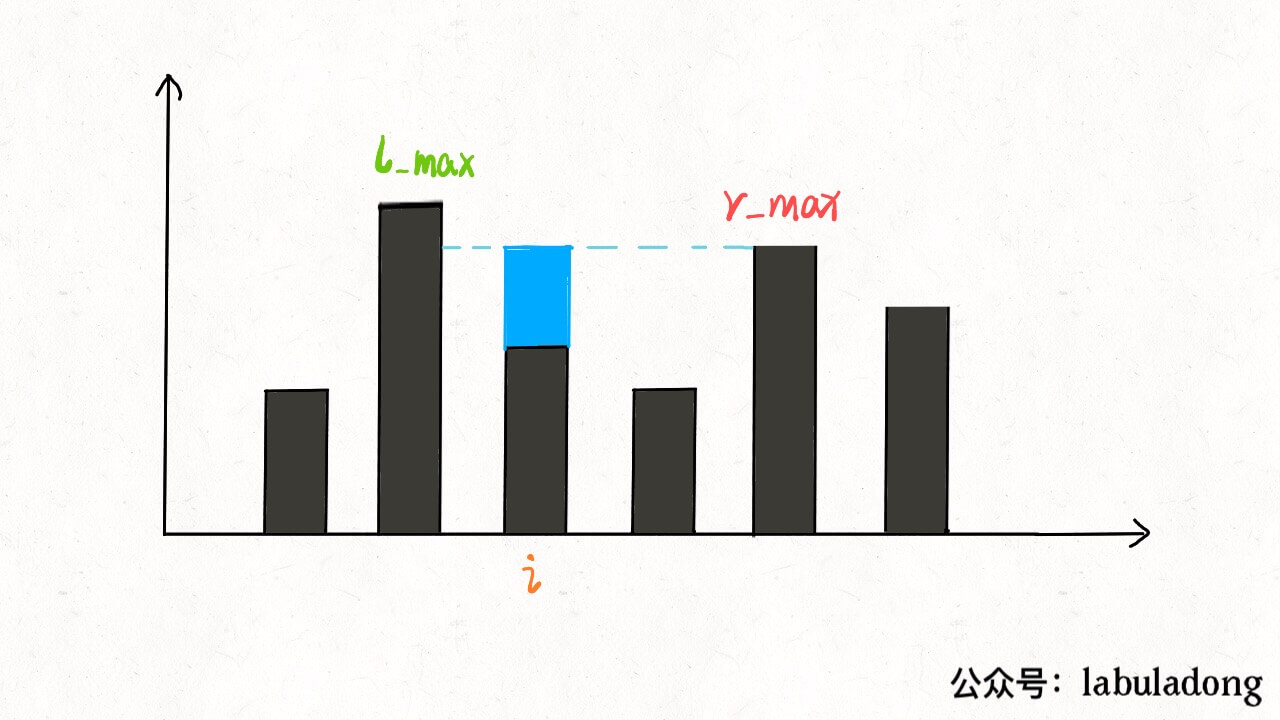
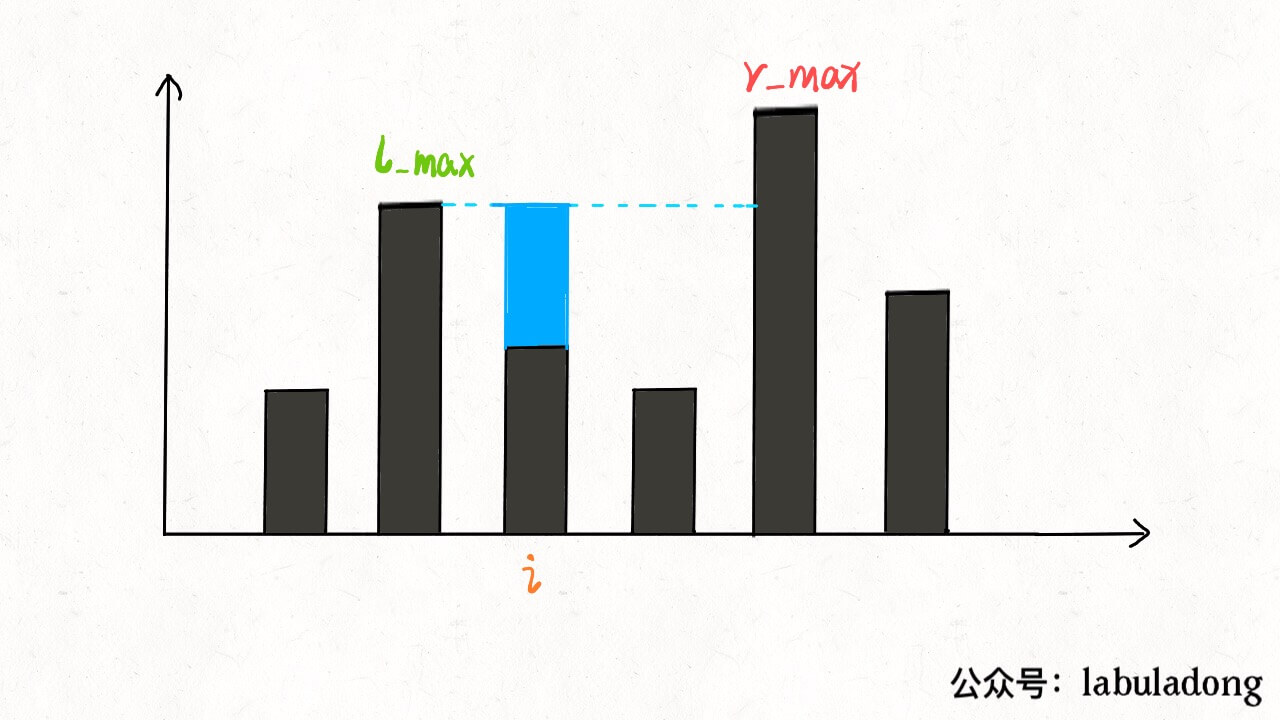
一、核心思路

我第一次看到这个问题，无计可施，完全没有思路，相信很多朋友跟我一样。所以对于这种问题，我们不要想整体，而应该去想局部；就像之前的文章处理字符串问题，不要考虑如何处理整个字符串，而是去思考应该如何处理每一个字符。
这么一想，可以发现这道题的思路其实很简单。具体来说，仅仅对于位置 i，能装下多少水呢？

能装 2 格水。为什么恰好是两格水呢？因为 height[i] 的高度为 0，而这里最多能盛 2 格水，2-0=2。
为什么位置 i 最多能盛 2 格水呢？因为，位置 i 能达到的水柱高度和其左边的最高柱子、右边的最高柱子有关，我们分别称这两个柱子高度为 l_max 和 r_max；位置 i 最大的水柱高度就是 min(l_max, r_max)。
更进一步，对于位置 i，能够装的水为：

1
2
3
4
5
6
7
water[i] = min(
               # 左边最高的柱子
               max(height[0..i]),  
               # 右边最高的柱子
               max(height[i..end]) 
            ) - height[i]



这就是本问题的核心思路，我们可以简单写一个暴力算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int trap(vector<int>& height) {
    int n = height.size();
    int ans = 0;
    for (int i = 1; i < n - 1; i++) {
        int l_max = 0, r_max = 0;
        // 找右边最高的柱子
        for (int j = i; j < n; j++)
            r_max = max(r_max, height[j]);
        // 找左边最高的柱子
        for (int j = i; j >= 0; j--)
            l_max = max(l_max, height[j]);
        // 如果自己就是最高的话，
        // l_max == r_max == height[i]
        ans += min(l_max, r_max) - height[i];
    }
    return ans;
}

有之前的思路，这个解法应该是很直接粗暴的，时间复杂度 O(N^2)，空间复杂度 O(1)。但是很明显这种计算 r_max 和 l_max 的方式非常笨拙，一般的优化方法就是备忘录。

二、备忘录优化

之前的暴力解法，不是在每个位置 i 都要计算 r_max 和 l_max 吗？我们直接把结果都缓存下来，别傻不拉几的每次都遍历，这时间复杂度不就降下来了嘛。
我们开两个数组 r_max 和 l_max 充当备忘录，l_max[i] 表示位置 i 左边最高的柱子高度，r_max[i] 表示位置 i 右边最高的柱子高度。预先把这两个数组计算好，避免重复计算：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int trap(vector<int>& height) {
    if (height.empty()) return 0;
    int n = height.size();
    int ans = 0;
    // 数组充当备忘录
    vector<int> l_max(n), r_max(n);
    // 初始化 base case
    l_max[0] = height[0];
    r_max[n - 1] = height[n - 1];
    // 从左向右计算 l_max
    for (int i = 1; i < n; i++)
        l_max[i] = max(height[i], l_max[i - 1]);
    // 从右向左计算 r_max
    for (int i = n - 2; i >= 0; i--) 
        r_max[i] = max(height[i], r_max[i + 1]);
    // 计算答案
    for (int i = 1; i < n - 1; i++) 
        ans += min(l_max[i], r_max[i]) - height[i];
    return ans;
}

这个优化其实和暴力解法差不多，就是避免了重复计算，把时间复杂度降低为 O(N)，已经是最优了，但是空间复杂度是 O(N)。下面来看一个精妙一些的解法，能够把空间复杂度降低到 O(1)。

三、双指针解法

这种解法的思路是完全相同的，但在实现手法上非常巧妙，我们这次也不要用备忘录提前计算了，而是用双指针边走边算，节省下空间复杂度。
首先，看一部分代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
int trap(vector<int>& height) {
    int n = height.size();
    int left = 0, right = n - 1;
    
    int l_max = height[0];
    int r_max = height[n - 1];
    
    while (left <= right) {
        l_max = max(l_max, height[left]);
        r_max = max(r_max, height[right]);
        left++; right--;
    }
}

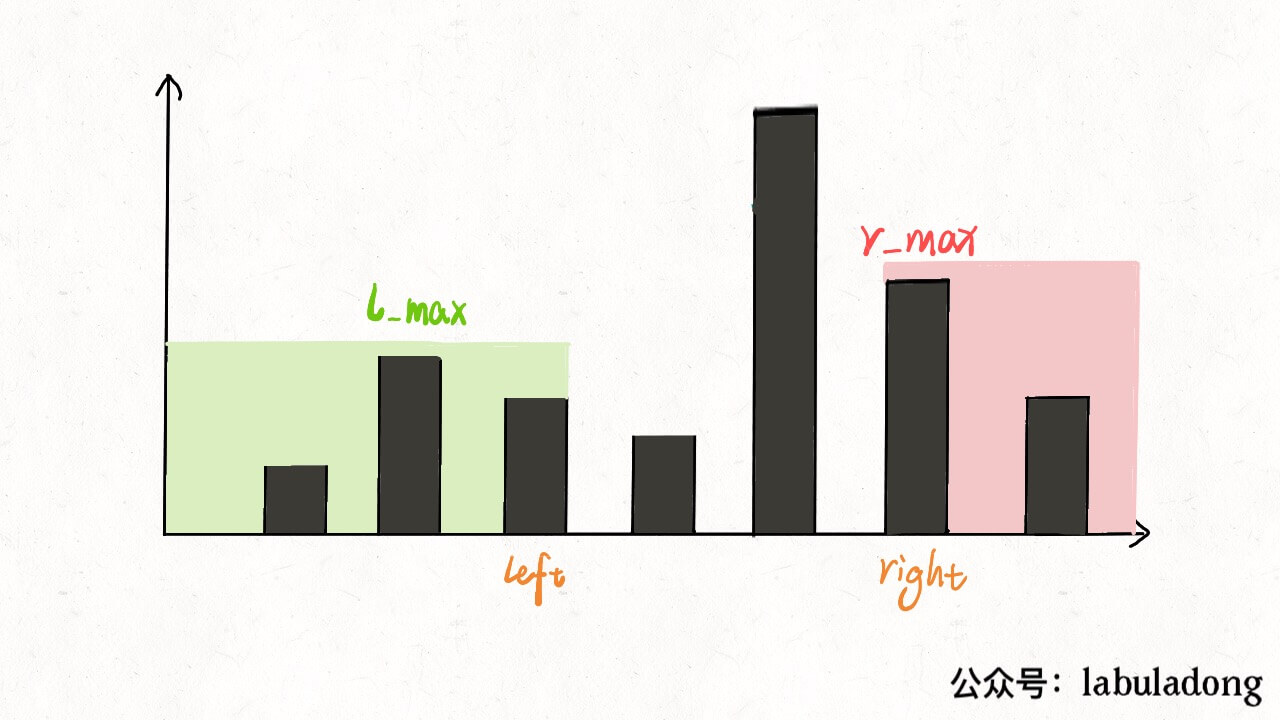
对于这部分代码，请问 l_max 和 r_max 分别表示什么意义呢？
很容易理解，**l_max 是 height[0..left] 中最高柱子的高度，r_max 是 height[right..end] 的最高柱子的高度**。
明白了这一点，直接看解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int trap(vector<int>& height) {
    if (height.empty()) return 0;
    int n = height.size();
    int left = 0, right = n - 1;
    int ans = 0;
    
    int l_max = height[0];
    int r_max = height[n - 1];
    
    while (left <= right) {
        l_max = max(l_max, height[left]);
        r_max = max(r_max, height[right]);
        
        // ans += min(l_max, r_max) - height[i]
        if (l_max < r_max) {
            ans += l_max - height[left];
            left++; 
        } else {
            ans += r_max - height[right];
            right--;
        }
    }
    return ans;
}

你看，其中的核心思想和之前一模一样，换汤不换药。但是细心的读者可能会发现次解法还是有点细节差异：
之前的备忘录解法，l_max[i] 和 r_max[i] 代表的是 height[0..i] 和 height[i..end] 的最高柱子高度。

1
ans += min(l_max[i], r_max[i]) - height[i];


但是双指针解法中，l_max 和 r_max 代表的是 height[0..left] 和 height[right..end] 的最高柱子高度。比如这段代码：

1
2
3
4
if (l_max < r_max) {
    ans += l_max - height[left];
    left++; 
}


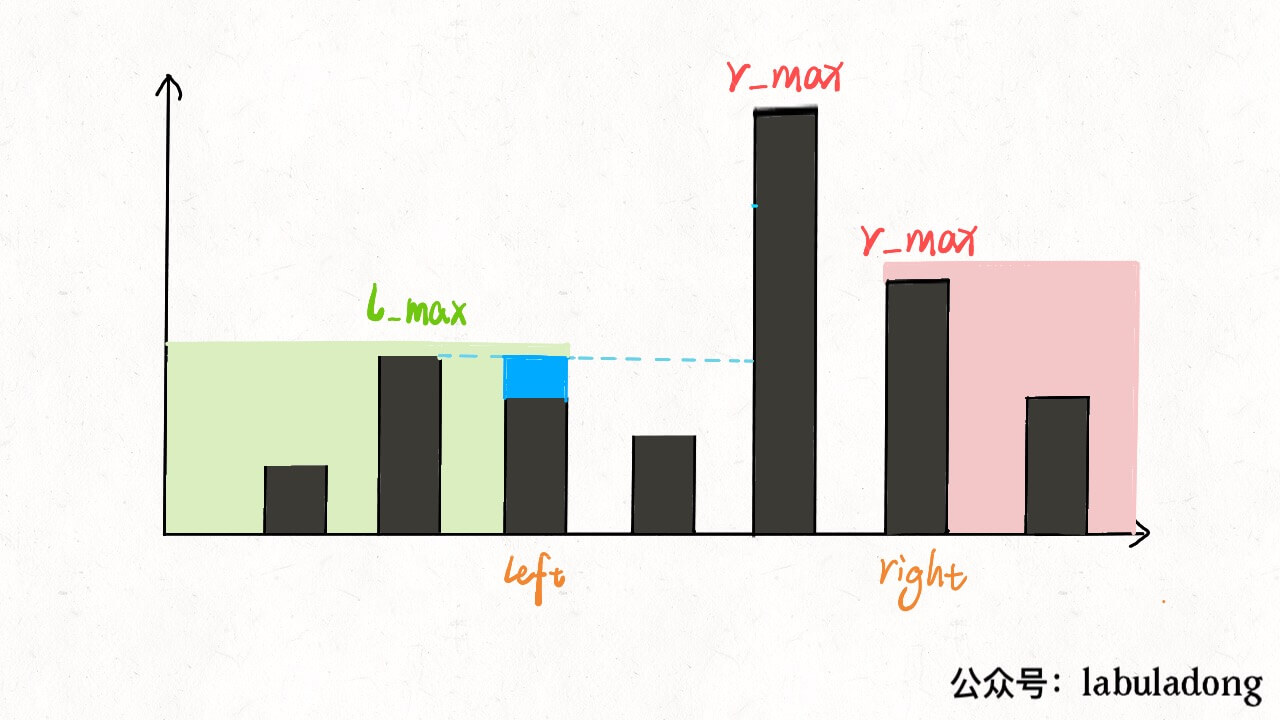
此时的 l_max 是 left 指针左边的最高柱子，但是 r_max 并不一定是 left 指针右边最高的柱子，这真的可以得到正确答案吗？
其实这个问题要这么思考，我们只在乎 min(l_max, r_max)。对于上图的情况，我们已经知道 l_max < r_max 了，至于这个 r_max 是不是右边最大的，不重要，重要的是 height[i] 能够装的水只和 l_max 有关。

上一篇：如何运用二分查找算法
下一篇：如何去除有序数组的重复元素
目录