虽说我没事就喜欢喷应试教育，但我也从应试教育中发现了一个窍门：如果能够以刷题的形式学习某项技能，效率和效果是最佳的。对于技术的学习，我经常面临的困境是，理论知识知道的不少，但是有的场景实在无法模拟，缺少亲自动手实践的机会，如果能有一本带标准答案的习题册让我刷刷就好了。
所以在学习新技术时，我首先会去搜索是否有在线刷题平台，你还别说，有的大神真就做了很不错的在线练习平台，下面就介绍几个平台，分别是学习 Git、SQL、正则表达式的在线练习平台。

一、练习 Git

这是个叫做 Learning Git Branching 的项目，是我一定要推荐的：

正如对话框中的自我介绍，这确实也是我至今发现的最好的 Git 动画教程，没有之一。
想当年我用 Git 就会 add .，clone，push，pull，commit 几个命令，其他的命令完全不会，Git 就是一个下载器，Github 就是个资源网站加免费图床，命令能不能达成目的都是靠运气。什么版本控制，我根本搞不懂，也懒得去看那一堆乱七八糟的文档。
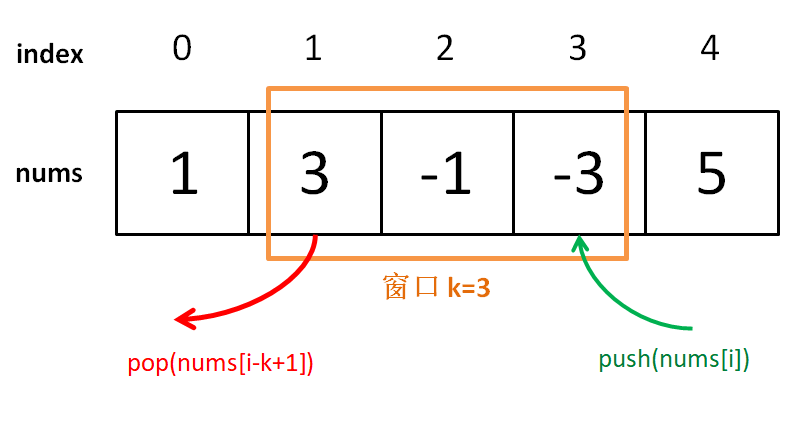
这个网站的教程不是给你举那种修改文件的细节例子，而是将每次 commit 都抽象成树的节点，用动画闯关的形式，让你自由使用 Git 命令完成目标：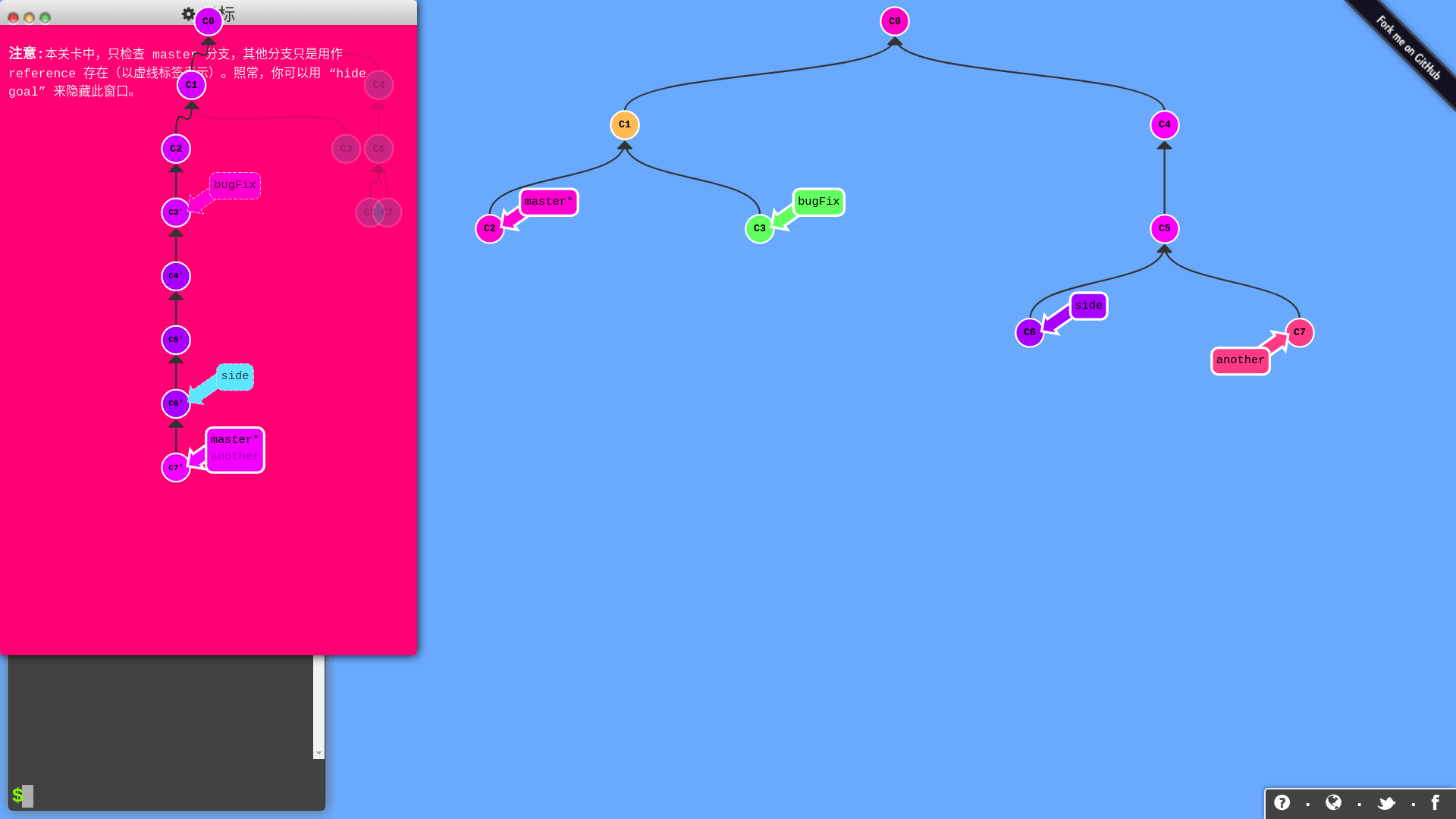

所有 Git 分支都被可视化了，你只要在左侧的命令行输入 Git 命令，分支会进行相应的变化，只要达成任务目标，你就过关啦！网站还会记录你的命令数，试试能不能以最少的命令数过关！

我一开始以为这个教程只包含本地 Git 仓库的版本管理，后来我惊奇地发现它还有远程仓库的操作教程！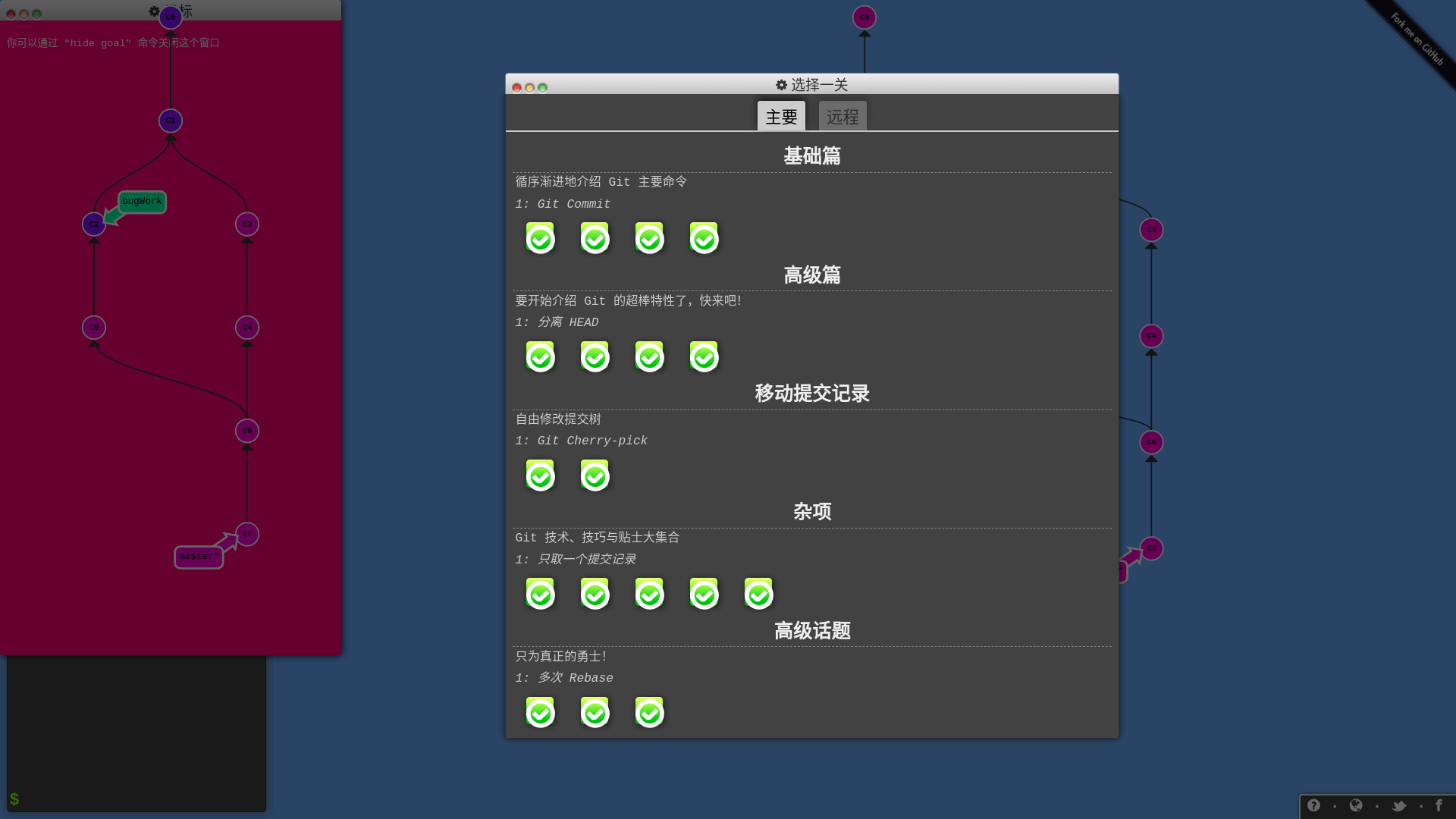


真的跟玩游戏一样，难度设计合理，流畅度很好，我一玩都停不下来了，几小时就打通了，哈哈哈！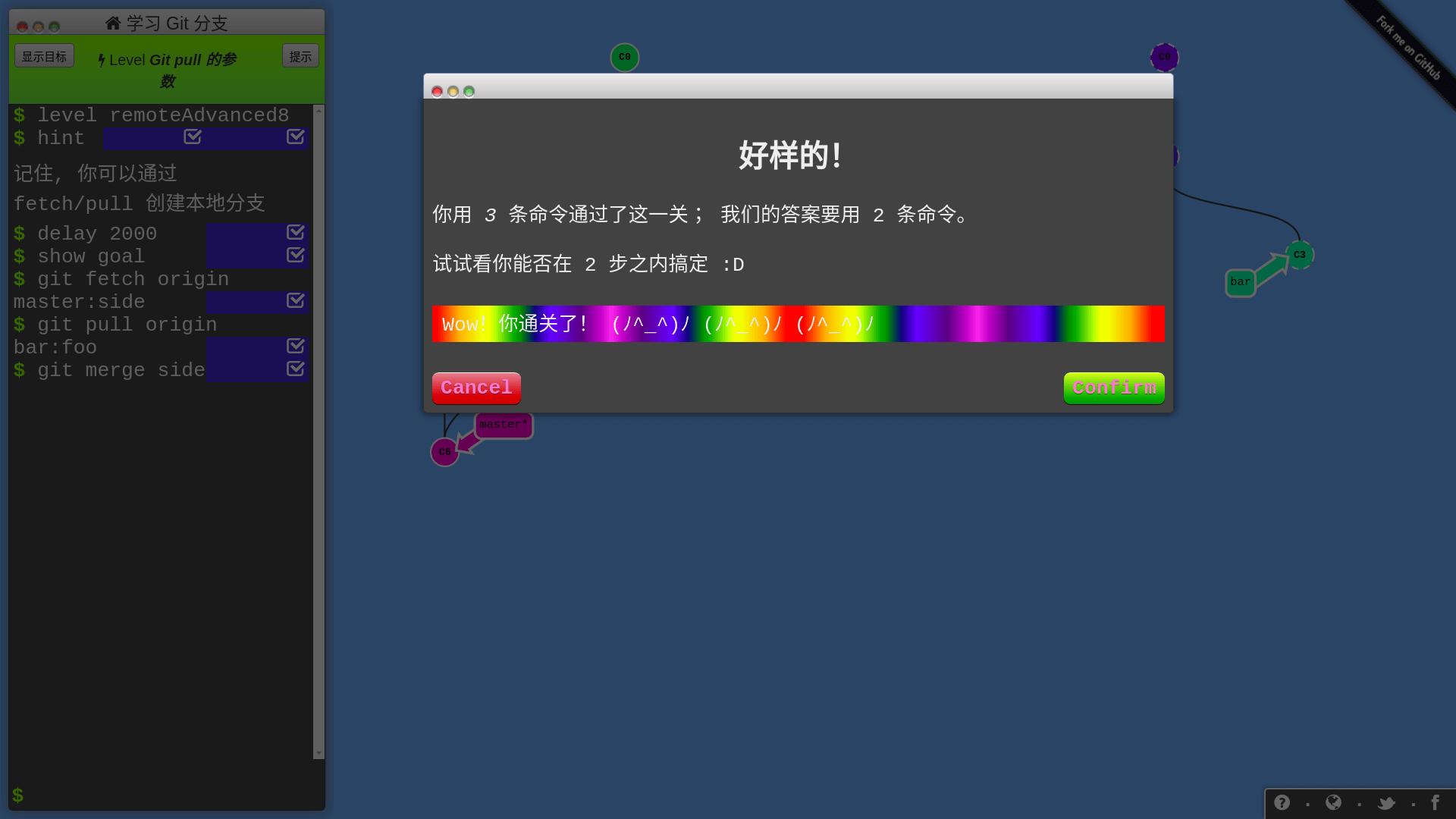

总之，这个教程很适合初学和进阶，如果你觉得自己对 Git 的掌握还不太好，用 Git 命令还是靠碰运气，就可以玩玩这个教程，相信能够让你更熟练地使用 Git。
它是一个开源项目，Github 项目地址：
https://github.com/pcottle/learnGitBranching
教程网站地址：
https://learngitbranching.js.org

二、练习正则表达式

正则表达式是个非常强有力的工具，可以说计算机中的一切数据都是字符，借助正则表达式这种模式匹配工具，操作计算机可以说是如虎添翼。
我这里要推荐两个网站，一个是练习平台，一个是测试正则表达式的平台。
先说练习平台，叫做 RegexOne：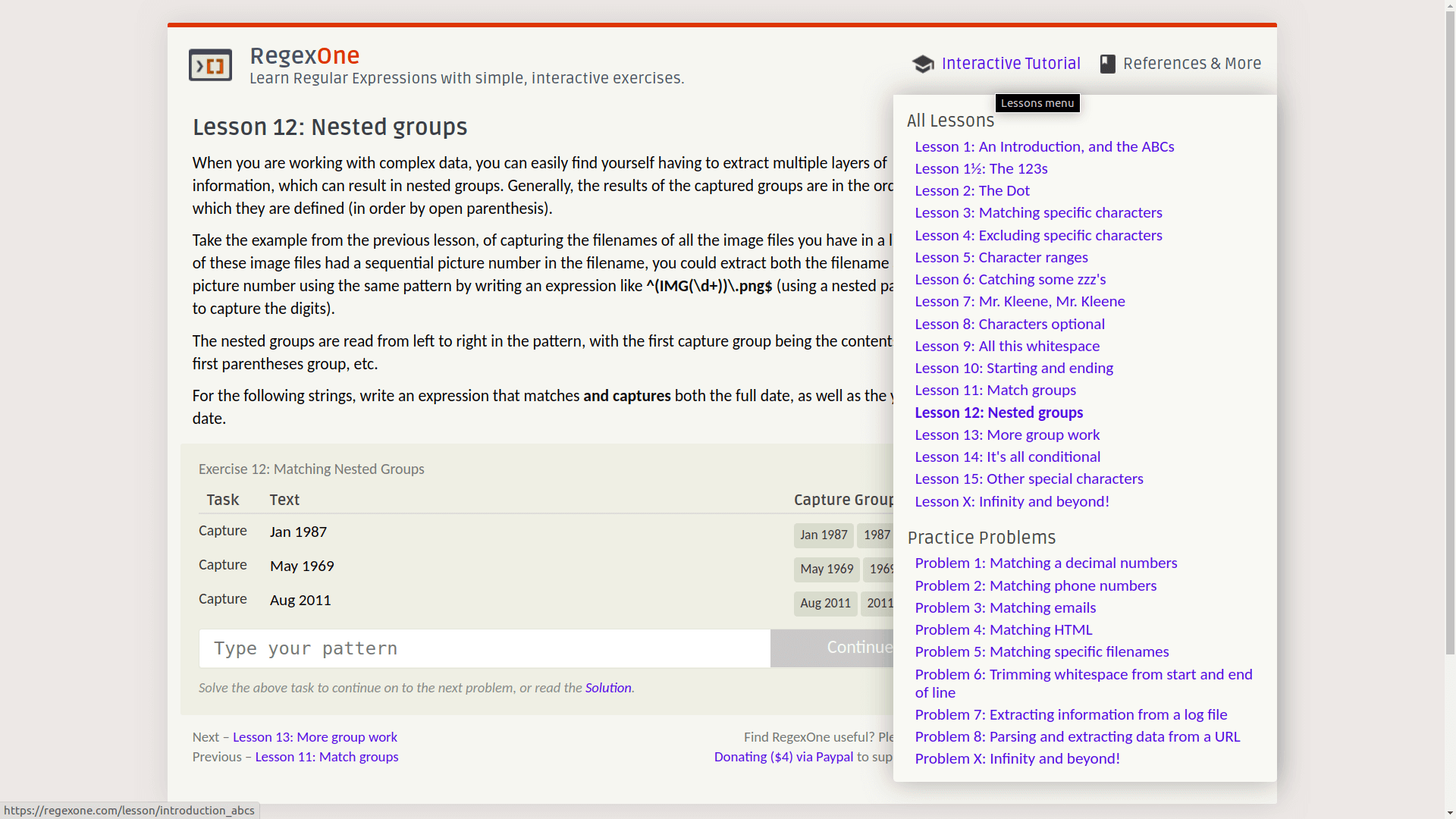

前面有基本教程，后面有一些常见的正则表达式题目，比如判断邮箱、URL、电话号，或者抽取日志的关键信息等等。
只要写出符合要求的正则表达式，就可以进入下一个问题，关键是每道题还有标准答案，可以点击下面的 solution 按钮查看：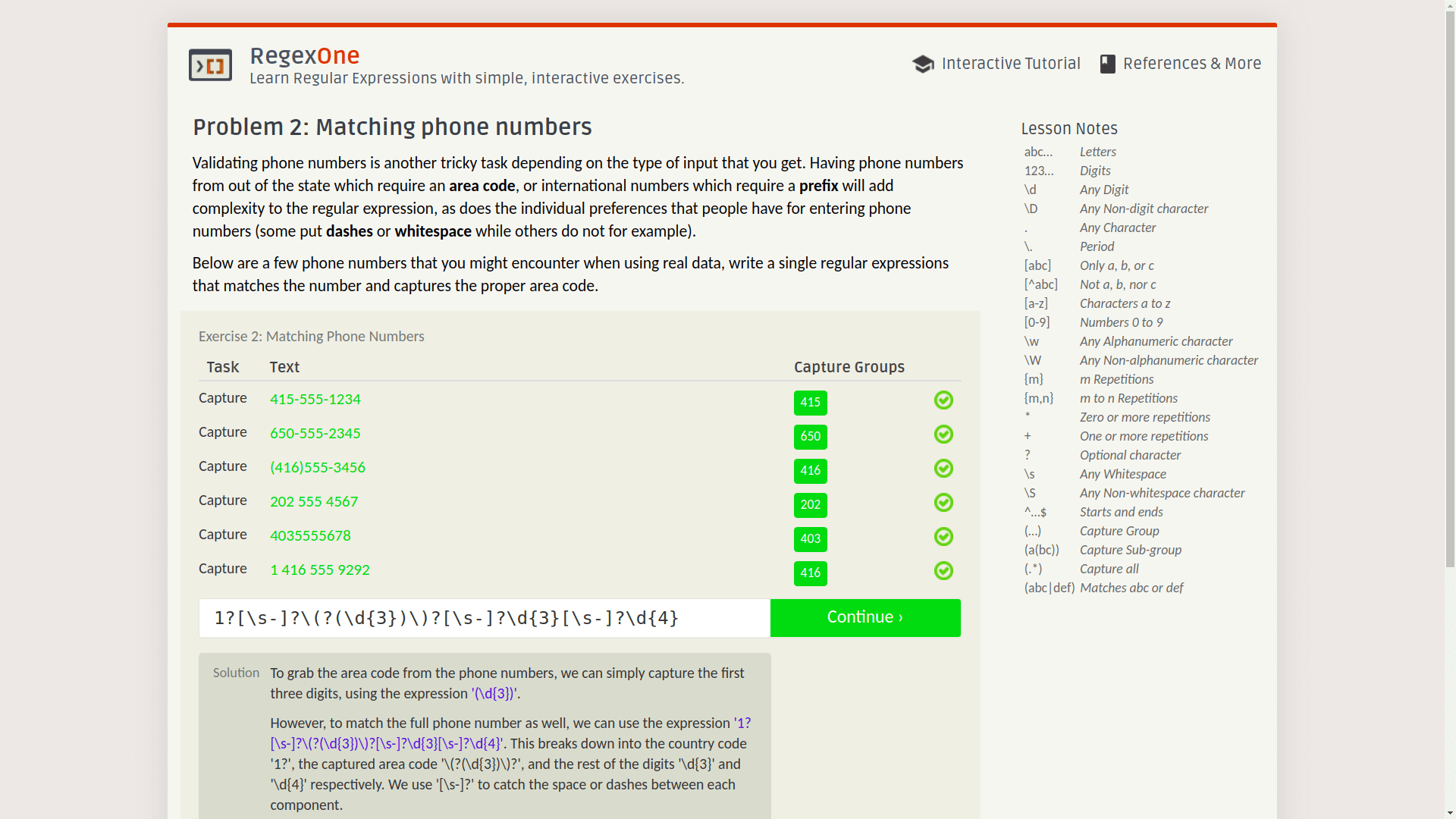

RegexOne 网址：
https://regexone.com/
再说测试工具，是个叫做 RegExr 的 Github 项目，这是它的网站：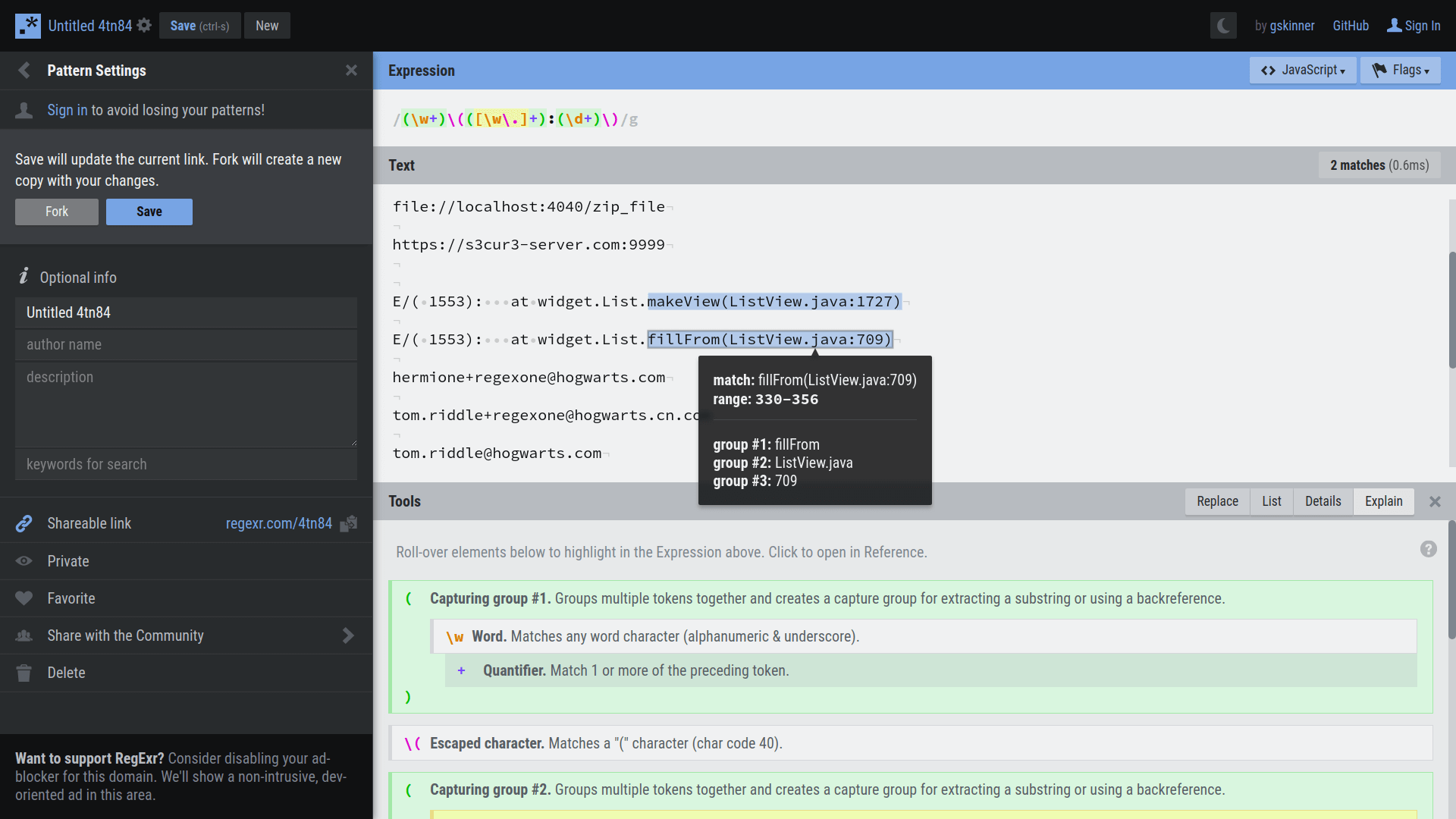

可以看见，输入文本和正则模式串后，网站会给正则表达式添加好看且容易辨认的样式，自动在文本中搜索模式串，高亮显示匹配的字符串，并且还会显示每个分组捕获的字符串。
这个网站可以配合前面的正则练习平台使用，在这里尝试各种表达式，成功匹配之后粘贴过去。
RegExr 网址：
https://regexr.com/

三、练习 SQL

这是一个叫做 SQLZOO 的网站，左侧是所有的练习内容：

SQLZOO 是一款很好用的 SQL 练习平台，英文不难理解，可以直接看英文版，但是也可以切换繁体中文，比较友好。
这里都是比较常用的 SQL 命令，给你一个需求，你写 SQL 语句实现正确的查询结果。最重要的是，这里不仅对每个命令的用法有详细解释，每个专题后面还有选择题（quiz），而且有判题系统，甚至有的比较难的题目还有视频讲解：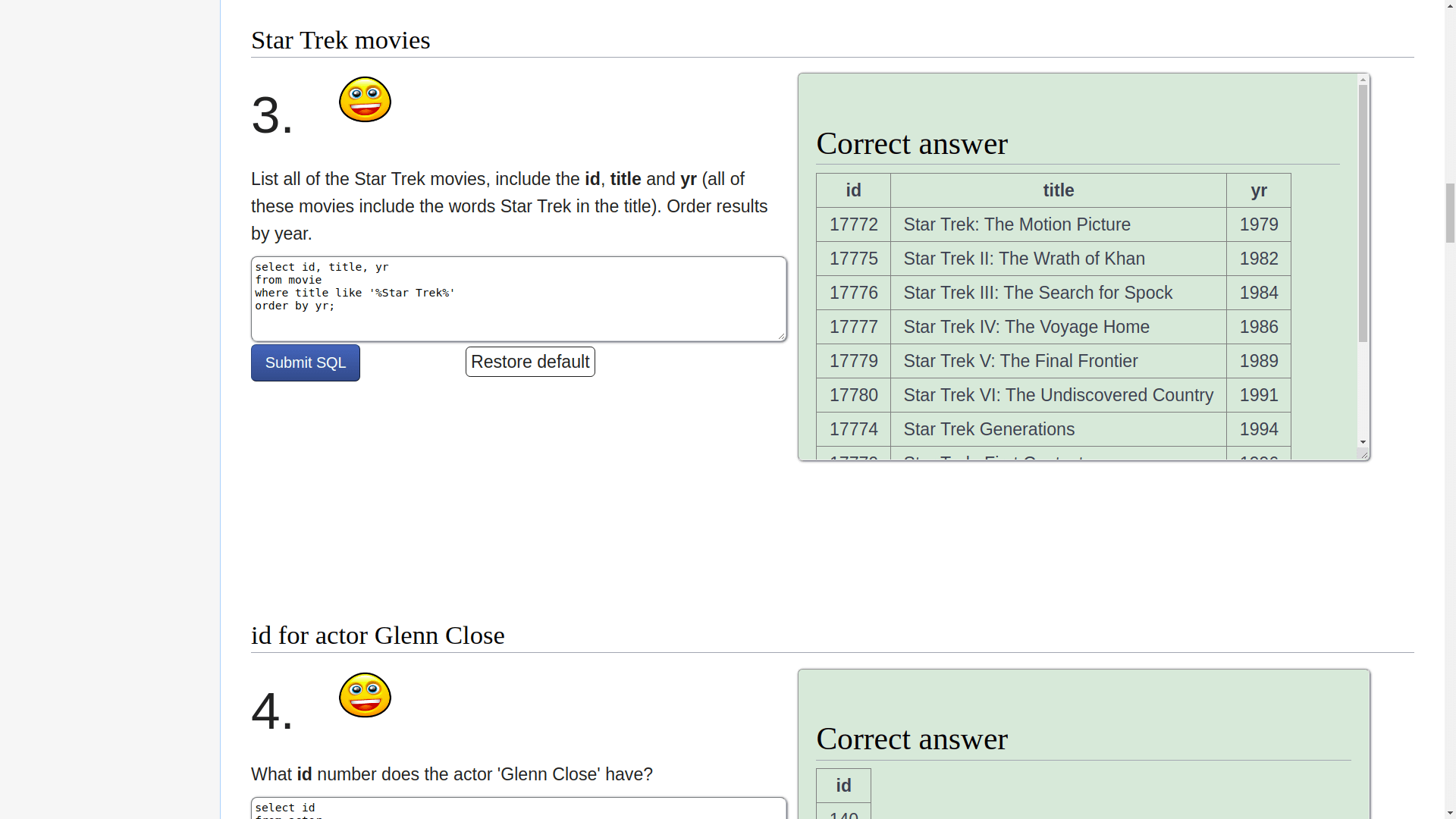

至于难度，循序渐进，即便对新手也很友好，靠后的问题确实比较有技巧性，相信这是热爱思维挑战的人喜欢的！LeetCode 也有 SQL 相关的题目，不过难度一般比较大，我觉得 SQLZOO 刷完基础 SQL 命令再去 LeetCode 刷比较合适。
网站地址：
https://sqlzoo.net/

上一篇：Linux的进程、线程、文件描述符是什么
下一篇：动态规划详解
目录

cookie 大家应该都熟悉，比如说登录某些网站一段时间后，就要求你重新登录；再比如有的同学很喜欢玩爬虫技术，有时候网站就是可以拦截住你的爬虫，这些都和 cookie 有关。如果你明白了服务器后端对于 cookie 和 session 的处理逻辑，就可以解释这些现象，甚至钻一些空子无限白嫖，待我慢慢道来。

一、session 和 cookie 简介

cookie 的出现是因为 HTTP 是无状态的一种协议，换句话说，服务器记不住你，可能你每刷新一次网页，就要重新输入一次账号密码进行登录。这显然是让人无法接受的，cookie 的作用就好比服务器给你贴个标签，然后你每次向服务器再发请求时，服务器就能够 cookie 认出你。
抽象地概括一下：一个 cookie 可以认为是一个「变量」，形如 name=value，存储在浏览器；一个 session 可以理解为一种数据结构，多数情况是「映射」（键值对），存储在服务器上。
注意，我说的是「一个」cookie 可以认为是一个变量，但是服务器可以一次设置多个 cookie，所以有时候说 cookie 是「一组」键值对儿，这也可以说得通。
cookie 可以在服务器端通过 HTTP 的 SetCookie 字段设置 cookie，比如我用 Go 语言写的一个简单服务：

1
2
3
4
5
6
7
8
9
10
11
12
13

func cookie(w http.ResponseWriter, r *http.Request) {
    // 设置了两个 cookie 
	http.SetCookie(w, &http.Cookie{
		Name:       "name1",
		Value:      "value1",
	})
	http.SetCookie(w, &http.Cookie{
		Name:  "name2",
		Value: "value2",
	})
    // 将字符串写入网页
	fmt.Fprintln(w, "页面内容")
}

当浏览器访问对应网址时，通过浏览器的开发者工具查看此次 HTTP 通信的细节，可以看见服务器的回应发出了两次 SetCookie 命令：

在这之后，浏览器的请求中的 Cookie 字段就带上了这两个 cookie：

cookie 的作用其实就是这么简单，无非就是服务器给每个客户端（浏览器）打的标签，方便服务器辨认而已。当然，HTTP 还有很多参数可以设置 cookie，比如过期时间，或者让某个 cookie 只有某个特定路径才能使用等等。
但问题是，我们也知道现在的很多网站功能很复杂，而且涉及很多的数据交互，比如说电商网站的购物车功能，信息量大，而且结构也比较复杂，无法通过简单的 cookie 机制传递这么多信息，而且要知道 cookie 字段是存储在 HTTP header 中的，就算能够承载这些信息，也会消耗很多的带宽，比较消耗网络资源。
session 就可以配合 cookie 解决这一问题，比如说一个 cookie 存储这样一个变量 sessionID=xxxx，仅仅把这一个 cookie 传给服务器，然后服务器通过这个 ID 找到对应的 session，这个 session 是一个数据结构，里面存储着该用户的购物车等详细信息，服务器可以通过这些信息返回该用户的定制化网页，有效解决了追踪用户的问题。
session 是一个数据结构，由网站的开发者设计，所以可以承载各种数据，只要客户端的 cookie 传来一个唯一的 session ID，服务器就可以找到对应的 session，认出这个客户。
当然，由于 session 存储在服务器中，肯定会消耗服务器的资源，所以 session 一般都会有一个过期时间，服务器一般会定期检查并删除过期的 session，如果后来该用户再次访问服务器，可能就会面临重新登录等等措施，然后服务器新建一个 session，将 session ID 通过 cookie 的形式传送给客户端。
那么，我们知道 cookie 和 session 的原理，有什么切实的好处呢？除了应对面试，我给你说一个鸡贼的用处，就是可以白嫖某些服务。
有些网站，你第一次使用它的服务，它直接免费让你试用，但是用一次之后，就让你登录然后付费继续使用该服务。而且你发现网站似乎通过某些手段记住了你的电脑，除非你换个电脑或者换个浏览器才能再白嫖一次。
那么问题来了，你试用的时候没有登录，网站服务器是怎么记住你的呢？这就很显然了，服务器一定是给你的浏览器打了 cookie，后台建立了对应的 session 记录你的状态。你的浏览器在每次访问该网站的时候都会听话地带着 cookie，服务器一查 session 就知道这个浏览器已经免费使用过了，得让它登录付费，不能让它继续白嫖了。
那如果我不让浏览器发送 cookie，每次都伪装成一个第一次来试用的小萌新，不就可以不断白嫖了么？浏览器会把网站的 cookie 以文件的形式存在某些地方（不同的浏览器配置不同），你把他们找到然后删除就行了。但是对于 Firefox 和 Chrome 浏览器，有很多插件可以直接编辑 cookie，比如我的 Chrome 浏览器就用的一款叫做 EditThisCookie 的插件，这是他们官网：

这类插件可以读取浏览器在当前网页的 cookie，点开插件可以任意编辑和删除 cookie。当然，偶尔白嫖一两次还行，不鼓励高频率白嫖，想常用还是掏钱吧，否则网站赚不到钱，就只能取消免费试用这个机制了。
以上就是关于 cookie 和 session 的简单介绍，cookie 是 HTTP 协议的一部分，不算复杂，而 session 是可以定制的，所以下面详细看一下实现 session 管理的代码架构吧。

二、session 的实现

session 的原理不难，但是具体实现它可是很有技巧的，一般需要三个组件配合完成，它们分别是 Manager、Provider 和 Session 三个类（接口）。

1、浏览器通过 HTTP 协议向服务器请求路径 /content 的网页资源，对应路径上有一个 Handler 函数接收请求，解析 HTTP header 中的 cookie，得到其中存储的 sessionID，然后把这个 ID 发给 Manager。
2、Manager 充当一个 session 管理器的角色，主要存储一些配置信息，比如 session 的存活时间，cookie 的名字等等。而所有的 session 存在 Manager 内部的一个 Provider 中。所以 Manager 会把 sid（sessionID）传递给 Provider，让它去找这个 ID 对应的具体是哪个 session。
3、Provider 就是一个容器，最常见的应该就是一个散列表，将每个 sid 和对应的 session 一一映射起来。收到 Manager 传递的 sid 之后，它就找到 sid 对应的 session 结构，也就是 Session 结构，然后返回它。
4、Session 中存储着用户的具体信息，由 Handler 函数中的逻辑拿出这些信息，生成该用户的 HTML 网页，返回给客户端。
那么你也许会问，为什么搞这么麻烦，直接在 Handler 函数中搞一个哈希表，然后存储 sid 和 Session 结构的映射不就完事儿了？
这就是设计层面的技巧了，下面就来说说，为什么分成 Manager、Provider 和 Session。

先从最底层的 Session 说。既然 session 就是键值对，为啥不直接用哈希表，而是要抽象出这么一个数据结构呢？
第一，因为 Session 结构可能不止存储了一个哈希表，还可以存储一些辅助数据，比如 sid，访问次数，过期时间或者最后一次的访问时间，这样便于实现想 LRU、LFU 这样的算法。
第二，因为 session 可以有不同的存储方式。如果用编程语言内置的哈希表，那么 session 数据就是存储在内存中，如果数据量大，很容易造成程序崩溃，而且一旦程序结束，所有 session 数据都会丢失。所以可以有很多种 session 的存储方式，比如存入缓存数据库 Redis，或者存入 MySQL 等等。
因此，Session 结构提供一层抽象，屏蔽不同存储方式的差异，只要提供一组通用接口操纵键值对：

1
2
3
4
5
6
7
8

type Session interface {
    // 设置键值对
    Set(key, val interface{})
    // 获取 key 对应的值
    Get(key interface{}) interface{}
    // 删除键 key
	Delete(key interface{})
}

再说 Provider 为啥要抽象出来。我们上面那个图的 Provider 就是一个散列表，保存 sid 到 Session 的映射，但是实际中肯定会更加复杂。我们不是要时不时删除一些 session 吗，除了设置存活时间之外，还可以采用一些其他策略，比如 LRU 缓存淘汰算法，这样就需要 Provider 内部使用哈希链表这种数据结构来存储 session。
PS：关于 LRU 算法的奥妙，参见前文「LRU 算法详解」。
因此，Provider 作为一个容器，就是要屏蔽算法细节，以合理的数据结构和算法组织 sid 和 Session 的映射关系，只需要实现下面这几个方法实现对 session 的增删查改：

1
2
3
4
5
6
7
8
9
10
11
12

type Provider interface {
    // 新增并返回一个 session
    SessionCreate(sid string) (Session, error)
    // 删除一个 session
    SessionDestroy(sid string)
    // 查找一个 session
    SessionRead(sid string) (Session, error)
    // 修改一个session
    SessionUpdate(sid string)
    // 通过类似 LRU 的算法回收过期的 session
	SessionGC(maxLifeTime int64)
}

最后说 Manager，大部分具体工作都委托给 Session 和 Provider 承担了，Manager 主要就是一个参数集合，比如 session 的存活时间，清理过期 session 的策略，以及 session 的可用存储方式。Manager 屏蔽了操作的具体细节，我们可以通过 Manager 灵活地配置 session 机制。
综上，session 机制分成几部分的最主要原因就是解耦，实现定制化。我在 Github 上看过几个 Go 语言实现的 session 服务，源码都很简单，有兴趣的朋友可以学习学习：
https://github.com/alexedwards/scs
https://github.com/astaxie/build-web-application-with-golang

上一篇：Linux的进程、线程、文件描述符是什么
下一篇：关于 Linux shell 你必须知道的
目录

说到密码，我们第一个想到的就是登陆账户的密码，但是从密码学的角度来看，这种根本就不算合格的密码。
为什么呢，因为我们的账户密码，是依靠隐蔽性来达到加密作用：密码藏在我心里，你不知道，所以你登不上我的账户。
然而密码技术认为，「保密」信息总有一天会被扒出来，所以加密算法不应该依靠「保密」来保证机密性，而应该做到：即便知道了加密算法，依然无计可施。说的魔幻一点就是，告诉你我的密码，你依然不知道我的密码。

最玄学的就是 Diffie-Hellman 密钥交换算法，我当初就觉得很惊奇，两个人当着你的面互相报几个数字，他们就可以拥有一个共同的秘密，而你却根本不可能算出来这个秘密。下文会着重介绍一下这个算法。
本文讨论的密码技术要解决的主要是信息传输中的加密和解密问题。要假设数据传输过程是不安全的，所有信息都在被窃听的，所以发送端要把信息加密，接收方收到信息之后，肯定得知道如何解密。有意思的是，如果你能够让接收者知道如何解密，那么窃听者不是也能够知道如何解密了吗？
下面，我们会介绍对称加密算法、密钥交换算法、非对称加密算法、数字签名、公钥证书，看看解决安全传输问题的一路坎坷波折。

一、对称性加密

对称性密码，也叫共享密钥密码，顾名思义，这种加密方式用相同的密钥进行加密和解密。
比如我说一种最简单的对称加密的方法。首先我们知道信息都可以表示成 0/1 比特序列，也知道相同的两个比特序列做异或运算的结果为 0。
那么我们就可以生成一个长度和原始信息一样的随机比特序列作为密钥，然后用它对原始信息做异或运算，就生成了密文。反之，再用该密钥对密文做一次异或运算，就可以恢复原始信息。
这是一个简单例子，不过有些过于简单，有很多问题。比如密钥的长度和原始信息完全一致，如果原始信息很大，密钥也会一样大，而且生成大量真随机比特序列的计算开销也比较大。
当然，有很多更复杂优秀的对称加密算法解决了这些问题，比如 Rijndael 算法、三重 DES 算法等等。它们从算法上是无懈可击的，也就是拥有巨大的密钥空间，基本无法暴力破解，而且加密过程相对快速。
但是，一切对称加密算法的软肋在于密钥的配送。加密和解密用同一个密钥，发送方必须设法把密钥发送给接收方。如果窃听者有能力窃取密文，肯定也可以窃取密钥，那么再无懈可击的算法依然不攻自破。
所以，下面介绍两种解决密钥配送问题最常见的算法，分别是 Diffie-Hellman 密钥交换算法和非对称加密算法。

二、密钥交换算法

我们所说的密钥一般就是一个很大的数字，算法用这个数加密、解密。问题在于，信道是不安全的，所有发出的数据都会被窃取。换句话说，有没有一种办法，能够让两个人在众目睽睽之下，光明正大地交换一个秘密，把对称性密钥安全地送到接收方的手中？
Diffie-Hellman 密钥交换算法可以做到。准确的说，该算法并不是把一个秘密安全地「送给」对方，而是通过一些共享的数字，双方「心中」各自「生成」了一个相同的秘密，而且双方的这个秘密，是第三方窃听者无法生成的。
也许这就是传说中的心有灵犀一点通吧。
这个算法规则不算复杂，你甚至都可以找个朋友尝试一下共享秘密，等会我会简单画出它的基本流程。在此之前，需要明确一个问题：并不是所有运算都有逆运算。
最简单的例子就是我们熟知的单向散列函数，给一个数字 a 和一个散列函数 f，你可以很快计算出 f(a)，但是如果给你 f(a) 和 f，推出 a 是一件基本做不到的事。密钥交换算法之所以看起来如此玄幻，就是利用了这种不可逆的性质。
下面，看下密钥交换算法的流程是什么，按照命名惯例，准备执行密钥交换算法的双方称为 Alice 和 Bob，在网络中企图窃取他俩通信内容的坏人称为 Hack 吧。
首先，Alice 和 Bob 协商出两个数字 N 和 G 作为生成元，当然协商过程可以被窃听者 Hack 窃取，所以我把这两个数画到中间，代表三方都知道：

现在 Alice 和 Bob 心中各自想一个数字出来，分别称为 A 和 B 吧：

现在 Alice 将自己心里的这个数字 A 和 G 通过某些运算得出一个数 AG，然后发给 Bob；Bob 将自己心里的数 B 和 G 通过相同的运算得出一个数 BG，然后发给 Alice：

现在的情况变成这样了：

注意，类似刚才举的散列函数的例子，知道 AG 和 G，并不能反推出 A 是多少，BG 同理。
那么，Alice 可以通过 BG 和自己的 A 通过某些运算得到一个数 ABG，Bob 也可以通过 AG 和自己的 B 通过某些运算得到 ABG，这个数就是 Alice 和 Bob 共有的秘密。
而对于 Hack，可以窃取传输过程中的 G，AG，BG，但是由于计算不可逆，怎么都无法结合出 ABG 这个数字。

以上就是基本流程，至于具体的数字取值是有讲究的，运算方法在百度上很容易找到，限于篇幅我就不具体写了。
该算法可以在第三者窃听的前提下，算出一个别人无法算出的秘密作为对称性加密算法的密钥，开始对称加密的通信。
对于该算法，Hack 又想到一种破解方法，不是窃听 Alice 和 Bob 的通信数据，而是直接同时冒充 Alice 和 Bob 的身份，也就是我们说的「中间人攻击」：

这样，双方根本无法察觉在和 Hack 共享秘密，后果就是 Hack 可以解密甚至修改数据。
可见，密钥交换算法也不算完全解决了密钥配送问题，缺陷在于无法核实对方身份。所以密钥交换算法之前一般要核实对方身份，比如使用数字签名。

三、非对称加密

非对称加密的思路就是，干脆别偷偷摸摸传输密钥了，我把加密密钥和解密密钥分开，公钥用于加密，私钥用于解密。只把公钥传送给对方，然后对方开始给我发送加密的数据，我用私钥就可以解密。至于窃听者，拿到公钥和加密数据也没用，因为只有我手上的私钥才能解密。
可以这样想，私钥是钥匙，而公钥是锁，可以把锁公开出去，让别人把数据锁起来发给我；而钥匙一定要留在自己手里，用于解锁。我们常见的 RSA 算法就是典型的非对称加密算法，具体实现比较复杂，我就不写了，网上很多资料。
在实际应用中，非对称性加密的运算速度要比对称性加密慢很多的，所以传输大量数据时，一般不会用公钥直接加密数据，而是加密对称性加密的密钥，传输给对方，然后双方使用对称性加密算法传输数据。
需要注意的是，类似 Diffie-Hellman 算法，非对称加密算法也无法确定通信双方的身份，依然会遭到中间人攻击。比如 Hack 拦截 Bob 发出的公钥，然后冒充 Bob 的身份给 Alice 发送自己的公钥，那么不知情的 Alice 就会把私密数据用 Hack 的公钥加密，Hack 可以通过私钥解密窃取。
那么，Diffie-Hellman 算法和 RSA 非对称加密算法都可以一定程度上解决密钥配送的问题，也具有相同的缺陷，二者的应用场景有什么区别呢？
简单来说，根据两种算法的基本原理就可以看出来：
如果双方有一个对称加密方案，希望加密通信，而且不能让别人得到钥匙，那么可以使用 Diffie-Hellman 算法交换密钥。
如果你希望任何人都可以对信息加密，而只有你能够解密，那么就使用 RSA 非对称加密算法，公布公钥。
下面，我们尝试着解决认证发送方身份的问题。

四、数字签名

刚才说非对称加密，把公钥公开用于他人对数据加密然后发给你，只有用你手上对应的私钥才能将密文解密。其实，私钥也可用用来加密数据的，对于 RSA 算法，私钥加密的数据只有公钥才能解开。
数字签名也是利用了非对称性密钥的特性，但是和公钥加密完全颠倒过来：仍然公布公钥，但是用你的私钥加密数据，然后把加密的数据公布出去，这就是数字签名。
你可能问，这有什么用，公钥可以解开私钥加密，我还加密发出去，不是多此一举吗？
是的，但是数字签名的作用本来就不是保证数据的机密性，而是证明你的身份，证明这些数据确实是由你本人发出的。
你想想，你的私钥加密的数据，只有你的公钥才能解开，那么如果一份加密数据能够被你的公钥解开，不就说明这份数据是你（私钥持有者）本人发布的吗？
当然，加密数据仅仅是一个签名，签名应该和数据一同发出，具体流程应该是：
1、Bob 生成公钥和私钥，然后把公钥公布出去，私钥自己保留。
2、用私钥加密数据作为签名，然后将数据附带着签名一同发布出去。
3、Alice 收到数据和签名，需要检查此份数据是否是 Bob 所发出，于是用 Bob 之前发出的公钥尝试解密签名，将收到的数据和签名解密后的结果作对比，如果完全相同，说明数据没被篡改，且确实由 Bob 发出。
为什么 Alice 这么肯定呢，毕竟数据和签名是两部分，都可以被掉包呀？原因如下：
1、如果有人修改了数据，那么 Alice 解密签名之后，对比发现二者不一致，察觉出异常。
2、如果有人替换了签名，那么 Alice 用 Bob 的公钥只能解出一串乱码，显然和数据不一致。
3、也许有人企图修改数据，然后将修改之后的数据制成签名，使得 Alice 的对比无法发现不一致；但是一旦解开签名，就不可能再重新生成 Bob 的签名了，因为没有 Bob 的私钥。
综上，数字签名可以一定程度上认证数据的来源。之所以说是一定程度上，是因为这种方式依然可能受到中间人攻击。一旦涉及公钥的发布，接收方就可能收到中间人的假公钥，进行错误的认证，这个问题始终避免不了。
说来可笑，数字签名就是验证对方身份的一种方式，但是前提是对方的身份必须是真的… 这似乎陷入一个先有鸡还是先有蛋的死循环，要想确定对方的身份，必须有一个信任的源头，否则的话，再多的流程也只是在转移问题，而不是真正解决问题。

五、公钥证书

证书其实就是公钥 + 签名，由第三方认证机构颁发。引入可信任的第三方，是终结信任循环的一种可行方案。
证书认证的流程大致如下：
1、Bob 去可信任的认证机构证实本人真实身份，并提供自己的公钥。
2、Alice 想跟 Bob 通信，首先向认证机构请求 Bob 的公钥，认证机构会把一张证书（Bob 的公钥以及自己对其公钥的签名）发送给 Alice。
3、Alice 检查签名，确定该公钥确实由这家认证机构发送，中途未被篡改。
4、Alice 通过这个公钥加密数据，开始和 Bob 通信。

PS：以上只是为了说明，证书只需要安装一次，并不需要每次都向认证机构请求；一般是服务器直接给客户端发送证书，而不是认证机构。
也许有人问，Alice 要想通过数字签名确定证书的有效性，前提是要有该机构的（认证）公钥，这不是又回到刚才的死循环了吗？
我们安装的正规浏览器中都预存了正规认证机构的证书（包含其公钥），用于确认机构身份，所以说证书的认证是可信的。
Bob 向机构提供公钥的过程中，需要提供很多个人信息进行身份验证，比较严格，所以说也算是可靠的。
获得了 Bob 的可信公钥，Alice 和 Bob 之间的通信基于加密算法的保护，是完全无懈可击的。
现在的正规网站，大都使用 HTTPS 协议，就是在 HTTP 协议和 TCP 协议之间加了一个 SSL/TLS 安全层。在你的浏览器和网站服务器完成 TCP 握手后，SSL 协议层也会进行 SSL 握手交换安全参数，其中就包含该网站的证书，以便浏览器验证站点身份。SSL 安全层验证完成之后，上层的 HTTP 协议内容都会被加密，保证数据的安全传输。
这样一来，传统的中间人攻击就几乎没有了生存空间，攻击手段只能由技术缺陷转变为坑蒙拐骗。事实上，这种手段的效果反而更高效，比如我就发现网上不少下载网站发布的浏览器，不仅包含乱七八糟的导航和收藏网址，还包含一些不正规的认证机构证书。任何人都可以申请证书，这些不正规证书很可能造成安全隐患。

六、最后总结

对称性加密算法使用同一个密钥加密和解密，难以破解，加密速度较快，但是存在密钥配送问题。
Diffie-Hellman 密钥交换算法可以让双方「心有灵犀一点通」，一定程度解决密钥配送问题，但是无法验证通信方的身份，所以可能受到中间人攻击。
非对称性加密算法生成一对儿密钥，把加密和解密的工作分开了。
RSA 算法作为经典的非对称加密算法，有两种用途：如果用于加密，可以把公钥发布出去用于加密，只有自己的私钥可以解密，保证了数据的机密性；如果用于数字签名，把公钥发布出去后，用私钥加密数据作为签名，以证明该数据由私钥持有者所发送。但是无论那种用法，涉及公钥的发布，都无法避免中间人攻击。
公钥证书就是公钥 + 签名，由可信任的第三方认证机构颁发。由于正规浏览器都预装了可信的认证机构的公钥，所以可以有效防止中间人攻击。
HTTPS 协议中的 SSL/TLS 安全层会组合使用以上几种加密方式，所以说不要安装非正规的浏览器，不要乱安装未知来源的证书。
密码技术只是安全的一小部分，即便是通过正规机构认证的 HTTPS 站点，也不意味着可信任，只能说明其数据传输是安全的。技术永远不可能真正保护你，最重要的还是得提高个人的安全防范意识，多留心眼儿，谨慎处理敏感数据。

上一篇：关于 Linux shell 你必须知道的
下一篇：Git/SQL/正则表达式的在线练习平台
目录

二叉堆详解实现优先级队列

二叉堆（Binary Heap）没什么神秘，性质比二叉搜索树 BST 还简单。其主要操作就两个，sink（下沉）和 swim（上浮），用以维护二叉堆的性质。其主要应用有两个，首先是一种排序方法「堆排序」，第二是一种很有用的数据结构「优先级队列」。
本文就以实现优先级队列（Priority Queue）为例，通过图片和人类的语言来描述一下二叉堆怎么运作的。

一、二叉堆概览

首先，二叉堆和二叉树有啥关系呢，为什么人们总数把二叉堆画成一棵二叉树？
因为，二叉堆其实就是一种特殊的二叉树（完全二叉树），只不过存储在数组里。一般的链表二叉树，我们操作节点的指针，而在数组里，我们把数组索引作为指针：

1
2
3
4
5
6
7
8
9
10
11
12

// 父节点的索引
int parent(int root) {
    return root / 2;
}
// 左孩子的索引
int left(int root) {
    return root * 2;
}
// 右孩子的索引
int right(int root) {
    return root * 2 + 1;
}

画个图你立即就能理解了，注意数组的第一个索引 0 空着不用，

PS：因为数组索引是数组，为了方便区分，将字符作为数组元素。
你看到了，把 arr[1] 作为整棵树的根的话，每个节点的父节点和左右孩子的索引都可以通过简单的运算得到，这就是二叉堆设计的一个巧妙之处。为了方便讲解，下面都会画的图都是二叉树结构，相信你能把树和数组对应起来。
二叉堆还分为最大堆和最小堆。最大堆的性质是：每个节点都大于等于它的两个子节点。类似的，最小堆的性质是：每个节点都小于等于它的子节点。
两种堆核心思路都是一样的，本文以最大堆为例讲解。
对于一个最大堆，根据其性质，显然堆顶，也就是 arr[1] 一定是所有元素中最大的元素。

二、优先级队列概览

优先级队列这种数据结构有一个很有用的功能，你插入或者删除元素的时候，元素会自动排序，这底层的原理就是二叉堆的操作。
数据结构的功能无非增删查该，优先级队列有两个主要 API，分别是 insert 插入一个元素和 delMax 删除最大元素（如果底层用最小堆，那么就是 delMin）。
下面我们实现一个简化的优先级队列，先看下代码框架：
PS：为了清晰起见，这里用到 Java 的泛型，Key 可以是任何一种可比较大小的数据类型，你可以认为它是 int、char 等。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

public class MaxPQ
    <Key extends Comparable<Key>> {
    // 存储元素的数组
    private Key[] pq;
    // 当前 Priority Queue 中的元素个数
    private int N = 0;
    public MaxPQ(int cap) {
        // 索引 0 不用，所以多分配一个空间
        pq = (Key[]) new Comparable[cap + 1];
    }
    /* 返回当前队列中最大元素 */
    public Key max() {
        return pq[1];
    }
    /* 插入元素 e */
    public void insert(Key e) {...}
    /* 删除并返回当前队列中最大元素 */
    public Key delMax() {...}
    /* 上浮第 k 个元素，以维护最大堆性质 */
    private void swim(int k) {...}
    /* 下沉第 k 个元素，以维护最大堆性质 */
    private void sink(int k) {...}
    /* 交换数组的两个元素 */
    private void exch(int i, int j) {
        Key temp = pq[i];
        pq[i] = pq[j];
        pq[j] = temp;
    }
    /* pq[i] 是否比 pq[j] 小？ */
    private boolean less(int i, int j) {
        return pq[i].compareTo(pq[j]) < 0;
    }
    /* 还有 left, right, parent 三个方法 */
}

空出来的四个方法是二叉堆和优先级队列的奥妙所在，下面用图文来逐个理解。

三、实现 swim 和 sink

为什么要有上浮 swim 和下沉 sink 的操作呢？为了维护堆结构。
我们要讲的是最大堆，每个节点都比它的两个子节点大，但是在插入元素和删除元素时，难免破坏堆的性质，这就需要通过这两个操作来恢复堆的性质了。
对于最大堆，会破坏堆性质的有有两种情况：

1. 如果某个节点 A 比它的子节点（中的一个）小，那么 A 就不配做父节点，应该下去，下面那个更大的节点上来做父节点，这就是对 A 进行下沉。
2. 如果某个节点 A 比它的父节点大，那么 A 不应该做子节点，应该把父节点换下来，自己去做父节点，这就是对 A 的上浮。
   当然，错位的节点 A 可能要上浮（或下沉）很多次，才能到达正确的位置，恢复堆的性质。所以代码中肯定有一个 while 循环。
   细心的读者也许会问，这两个操作不是互逆吗，所以上浮的操作一定能用下沉来完成，为什么我还要费劲写两个方法？
   是的，操作是互逆等价的，但是最终我们的操作只会在堆底和堆顶进行（等会讲原因），显然堆底的「错位」元素需要上浮，堆顶的「错位」元素需要下沉。

上浮的代码实现：

1
2
3
4
5
6
7
8
9

private void swim(int k) {
    // 如果浮到堆顶，就不能再上浮了
    while (k > 1 && less(parent(k), k)) {
        // 如果第 k 个元素比上层大
        // 将 k 换上去
        exch(parent(k), k);
        k = parent(k);
    }
}

画个 GIF 看一眼就明白了：

下沉的代码实现：
下沉比上浮略微复杂一点，因为上浮某个节点 A，只需要 A 和其父节点比较大小即可；但是下沉某个节点 A，需要 A 和其两个子节点比较大小，如果 A 不是最大的就需要调整位置，要把较大的那个子节点和 A 交换。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

private void sink(int k) {
    // 如果沉到堆底，就沉不下去了
    while (left(k) <= N) {
        // 先假设左边节点较大
        int older = left(k);
        // 如果右边节点存在，比一下大小
        if (right(k) <= N && less(older, right(k)))
            older = right(k);
        // 结点 k 比俩孩子都大，就不必下沉了
        if (less(older, k)) break;
        // 否则，不符合最大堆的结构，下沉 k 结点
        exch(k, older);
        k = older;
    }
}

画个 GIF 看下就明白了：

至此，二叉堆的主要操作就讲完了，一点都不难吧，代码加起来也就十行。明白了 sink 和 swim 的行为，下面就可以实现优先级队列了。

四、实现 delMax 和 insert

这两个方法就是建立在 swim 和 sink 上的。
**insert 方法先把要插入的元素添加到堆底的最后，然后让其上浮到正确位置。**

1
2
3
4
5
6
7

public void insert(Key e) {
    N++;
    // 先把新元素加到最后
    pq[N] = e;
    // 然后让它上浮到正确的位置
    swim(N);
}

delMax 方法先把堆顶元素 A 和堆底最后的元素 B 对调，然后删除 A，最后让 B 下沉到正确位置。

1
2
3
4
5
6
7
8
9
10
11

public Key delMax() {
    // 最大堆的堆顶就是最大元素
    Key max = pq[1];
    // 把这个最大元素换到最后，删除之
    exch(1, N);
    pq[N] = null;
    N--;
    // 让 pq[1] 下沉到正确位置
    sink(1);
    return max;
}

至此，一个优先级队列就实现了，插入和删除元素的时间复杂度为 $O(logK)$，$K$ 为当前二叉堆（优先级队列）中的元素总数。因为我们时间复杂度主要花费在 sink 或者 swim 上，而不管上浮还是下沉，最多也就树（堆）的高度，也就是 log 级别。

五、最后总结

二叉堆就是一种完全二叉树，所以适合存储在数组中，而且二叉堆拥有一些特殊性质。
二叉堆的操作很简单，主要就是上浮和下沉，来维护堆的性质（堆有序），核心代码也就十行。
优先级队列是基于二叉堆实现的，主要操作是插入和删除。插入是先插到最后，然后上浮到正确位置；删除是调换位置后再删除，然后下沉到正确位置。核心代码也就十行。
也许这就是数据结构的威力，简单的操作就能实现巧妙的功能，真心佩服发明二叉堆算法的人！

上一篇：学习数据结构和算法读什么书
下一篇：LRU算法详解
目录

二叉搜索树操作集锦

通过之前的文章框架思维，二叉树的遍历框架应该已经印到你的脑子里了，这篇文章就来实操一下，看看框架思维是怎么灵活运用，秒杀一切二叉树问题的。
二叉树算法的设计的总路线：明确一个节点要做的事情，然后剩下的事抛给框架。

1
2
3
4
5
6

void traverse(TreeNode root) {
    // root 需要做什么？在这做。
    // 其他的不用 root 操心，抛给框架
    traverse(root.left);
    traverse(root.right);
}

举两个简单的例子体会一下这个思路，热热身。
1. 如何把二叉树所有的节点中的值加一？

1
2
3
4
5
6

void plusOne(TreeNode root) {
    if (root == null) return;
    root.val += 1;
    plusOne(root.left);
    plusOne(root.right);
}

2. 如何判断两棵二叉树是否完全相同？

1
2
3
4
5
6
7
8
9
10
11

boolean isSameTree(TreeNode root1, TreeNode root2) {
    // 都为空的话，显然相同
    if (root1 == null && root2 == null) return true;
    // 一个为空，一个非空，显然不同
    if (root1 == null || root2 == null) return false;
    // 两个都非空，但 val 不一样也不行
    if (root1.val != root2.val) return false;
    // root1 和 root2 该比的都比完了
    return isSameTree(root1.left, root2.left)
        && isSameTree(root1.right, root2.right);
}

借助框架，上面这两个例子不难理解吧？如果可以理解，那么所有二叉树算法你都能解决。

二叉搜索树（Binary Search Tree，简称 BST）是一种很常用的的二叉树。它的定义是：一个二叉树中，任意节点的值要大于等于左子树所有节点的值，且要小于等于右边子树的所有节点的值。
如下就是一个符合定义的 BST：

下面实现 BST 的基础操作：判断 BST 的合法性、增、删、查。其中“删”和“判断合法性”略微复杂。
零、判断 BST 的合法性
这里是有坑的哦，我们按照刚才的思路，每个节点自己要做的事不就是比较自己和左右孩子吗？看起来应该这样写代码：

1
2
3
4
5
6
7

boolean isValidBST(TreeNode root) {
    if (root == null) return true;
    if (root.left != null && root.val <= root.left.val) return false;
    if (root.right != null && root.val >= root.right.val) return false;
    return isValidBST(root.left)
        && isValidBST(root.right);
}

但是这个算法出现了错误，BST 的每个节点应该要小于右边子树的所有节点，下面这个二叉树显然不是 BST，但是我们的算法会把它判定为 BST。

出现错误，不要慌张，框架没有错，一定是某个细节问题没注意到。我们重新看一下 BST 的定义，root 需要做的不只是和左右子节点比较，而是要整个左子树和右子树所有节点比较。怎么办，鞭长莫及啊！
这种情况，我们可以使用辅助函数，增加函数参数列表，在参数中携带额外信息，请看正确的代码：

1
2
3
4
5
6
7
8
9
10

boolean isValidBST(TreeNode root) {
    return isValidBST(root, null, null);
}
boolean isValidBST(TreeNode root, TreeNode min, TreeNode max) {
    if (root == null) return true;
    if (min != null && root.val <= min.val) return false;
    if (max != null && root.val >= max.val) return false;
    return isValidBST(root.left, min, root) 
        && isValidBST(root.right, root, max);
}

一、在 BST 中查找一个数是否存在
根据我们的指导思想，可以这样写代码：

1
2
3
4
5
6

boolean isInBST(TreeNode root, int target) {
    if (root == null) return false;
    if (root.val == target) return true;
    return isInBST(root.left, target)
        || isInBST(root.right, target);
}

这样写完全正确，充分证明了你的框架性思维已经养成。现在你可以考虑一点细节问题了：如何充分利用信息，把 BST 这个“左小右大”的特性用上？
很简单，其实不需要递归地搜索两边，类似二分查找思想，根据 target 和 root.val 的大小比较，就能排除一边。我们把上面的思路稍稍改动：

1
2
3
4
5
6
7
8
9
10

boolean isInBST(TreeNode root, int target) {
    if (root == null) return false;
    if (root.val == target)
        return true;
    if (root.val < target) 
        return isInBST(root.right, target);
    if (root.val > target)
        return isInBST(root.left, target);
    // root 该做的事做完了，顺带把框架也完成了，妙
}

于是，我们对原始框架进行改造，抽象出一套针对 BST 的遍历框架：

1
2
3
4
5
6
7
8

void BST(TreeNode root, int target) {
    if (root.val == target)
        // 找到目标，做点什么
    if (root.val < target) 
        BST(root.right, target);
    if (root.val > target)
        BST(root.left, target);
}

二、在 BST 中插入一个数
对数据结构的操作无非遍历 + 访问，遍历就是“找”，访问就是“改”。具体到这个问题，插入一个数，就是先找到插入位置，然后进行插入操作。
上一个问题，我们总结了 BST 中的遍历框架，就是“找”的问题。直接套框架，加上“改”的操作即可。一旦涉及“改”，函数就要返回 TreeNode 类型，并且对递归调用的返回值进行接收。

1
2
3
4
5
6
7
8
9
10
11

TreeNode insertIntoBST(TreeNode root, int val) {
    // 找到空位置插入新节点
    if (root == null) return new TreeNode(val);
    // if (root.val == val)
    //     BST 中一般不会插入已存在元素
    if (root.val < val) 
        root.right = insertIntoBST(root.right, val);
    if (root.val > val) 
        root.left = insertIntoBST(root.left, val);
    return root;
}

三、在 BST 中删除一个数
这个问题稍微复杂，不过你有框架指导，难不住你。跟插入操作类似，先“找”再“改”，先把框架写出来再说：

1
2
3
4
5
6
7
8
9
10

TreeNode deleteNode(TreeNode root, int key) {
    if (root.val == key) {
        // 找到啦，进行删除
    } else if (root.val > key) {
        root.left = deleteNode(root.left, key);
    } else if (root.val < key) {
        root.right = deleteNode(root.right, key);
    }
    return root;
}

找到目标节点了，比方说是节点 A，如何删除这个节点，这是难点。因为删除节点的同时不能破坏 BST 的性质。有三种情况，用图片来说明。
情况 1：A 恰好是末端节点，两个子节点都为空，那么它可以当场去世了。
图片来自 LeetCode

1
2

if (root.left == null && root.right == null)
    return null;

情况 2：A 只有一个非空子节点，那么它要让这个孩子接替自己的位置。
图片来自 LeetCode

1
2
3

// 排除了情况 1 之后
if (root.left == null) return root.right;
if (root.right == null) return root.left;

情况 3：A 有两个子节点，麻烦了，为了不破坏 BST 的性质，A 必须找到左子树中最大的那个节点，或者右子树中最小的那个节点来接替自己。我们以第二种方式讲解。
图片来自 LeetCode

1
2
3
4
5
6
7
8

if (root.left != null && root.right != null) {
    // 找到右子树的最小节点
    TreeNode minNode = getMin(root.right);
    // 把 root 改成 minNode
    root.val = minNode.val;
    // 转而去删除 minNode
    root.right = deleteNode(root.right, minNode.val);
}

三种情况分析完毕，填入框架，简化一下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

TreeNode deleteNode(TreeNode root, int key) {
    if (root == null) return null;
    if (root.val == key) {
        // 这两个 if 把情况 1 和 2 都正确处理了
        if (root.left == null) return root.right;
        if (root.right == null) return root.left;
        // 处理情况 3
        TreeNode minNode = getMin(root.right);
        root.val = minNode.val;
        root.right = deleteNode(root.right, minNode.val);
    } else if (root.val > key) {
        root.left = deleteNode(root.left, key);
    } else if (root.val < key) {
        root.right = deleteNode(root.right, key);
    }
    return root;
}
TreeNode getMin(TreeNode node) {
    // BST 最左边的就是最小的
    while (node.left != null) node = node.left;
    return node;
} 

删除操作就完成了。注意一下，这个删除操作并不完美，因为我们一般不会通过 root.val = minNode.val 修改节点内部的值来交换节点，而是通过一系列略微复杂的链表操作交换 root 和 minNode 两个节点。因为具体应用中，val 域可能会很大，修改起来很耗时，而链表操作无非改一改指针，而不会去碰内部数据。
但这里忽略这个细节，旨在突出 BST 基本操作的共性，以及借助框架逐层细化问题的思维方式。
四、最后总结
通过这篇文章，你学会了如下几个技巧：

1. 二叉树算法设计的总路线：把当前节点要做的事做好，其他的交给递归框架，不用当前节点操心。
2. 如果当前节点会对下面的子节点有整体影响，可以通过辅助函数增长参数列表，借助参数传递信息。
3. 在二叉树框架之上，扩展出一套 BST 遍历框架：

   1 2 3 4 5 6 7 8

   void BST(TreeNode root, int target) { if (root.val == target) // 找到目标，做点什么 if (root.val < target) BST(root.right, target); if (root.val > target) BST(root.left, target); }

4. 掌握了 BST 的基本操作。

上一篇：LRU算法详解
下一篇：特殊数据结构：单调栈
目录

如何使用单调栈解题

栈（stack）是很简单的一种数据结构，先进后出的逻辑顺序，符合某些问题的特点，比如说函数调用栈。
单调栈实际上就是栈，只是利用了一些巧妙的逻辑，使得每次新元素入栈后，栈内的元素都保持有序（单调递增或单调递减）。
听起来有点像堆（heap）？不是的，单调栈用途不太广泛，只处理一种典型的问题，叫做 Next Greater Element。本文用讲解单调队列的算法模版解决这类问题，并且探讨处理「循环数组」的策略。
首先，讲解 Next Greater Number 的原始问题：给你一个数组，返回一个等长的数组，对应索引存储着下一个更大元素，如果没有更大的元素，就存 -1。不好用语言解释清楚，直接上一个例子：
给你一个数组 [2,1,2,4,3]，你返回数组 [4,2,4,-1,-1]。
解释：第一个 2 后面比 2 大的数是 4; 1 后面比 1 大的数是 2；第二个 2 后面比 2 大的数是 4; 4 后面没有比 4 大的数，填 -1；3 后面没有比 3 大的数，填 -1。
这道题的暴力解法很好想到，就是对每个元素后面都进行扫描，找到第一个更大的元素就行了。但是暴力解法的时间复杂度是 O(n^2)。
这个问题可以这样抽象思考：把数组的元素想象成并列站立的人，元素大小想象成人的身高。这些人面对你站成一列，如何求元素「2」的 Next Greater Number 呢？很简单，如果能够看到元素「2」，那么他后面可见的第一个人就是「2」的 Next Greater Number，因为比「2」小的元素身高不够，都被「2」挡住了，第一个露出来的就是答案。

这个情景很好理解吧？带着这个抽象的情景，先来看下代码。

1
2
3
4
5
6
7
8
9
10
11
12

vector<int> nextGreaterElement(vector<int>& nums) {
    vector<int> ans(nums.size()); // 存放答案的数组
    stack<int> s;
    for (int i = nums.size() - 1; i >= 0; i--) { // 倒着往栈里放
        while (!s.empty() && s.top() <= nums[i]) { // 判定个子高矮
            s.pop(); // 矮个起开，反正也被挡着了。。。
        }
        ans[i] = s.empty() ? -1 : s.top(); // 这个元素身后的第一个高个
        s.push(nums[i]); // 进队，接受之后的身高判定吧！
    }
    return ans;
}

这就是单调队列解决问题的模板。for 循环要从后往前扫描元素，因为我们借助的是栈的结构，倒着入栈，其实是正着出栈。while 循环是把两个“高个”元素之间的元素排除，因为他们的存在没有意义，前面挡着个“更高”的元素，所以他们不可能被作为后续进来的元素的 Next Great Number 了。
这个算法的时间复杂度不是那么直观，如果你看到 for 循环嵌套 while 循环，可能认为这个算法的复杂度也是 O(n^2)，但是实际上这个算法的复杂度只有 O(n)。
分析它的时间复杂度，要从整体来看：总共有 n 个元素，每个元素都被 push 入栈了一次，而最多会被 pop 一次，没有任何冗余操作。所以总的计算规模是和元素规模 n 成正比的，也就是 O(n) 的复杂度。
现在，你已经掌握了单调栈的使用技巧，来一个简单的变形来加深一下理解。
给你一个数组 T = [73, 74, 75, 71, 69, 72, 76, 73]，这个数组存放的是近几天的天气气温（这气温是铁板烧？不是的，这里用的华氏度）。你返回一个数组，计算：对于每一天，你还要至少等多少天才能等到一个更暖和的气温；如果等不到那一天，填 0 。
举例：给你 T = [73, 74, 75, 71, 69, 72, 76, 73]，你返回 [1, 1, 4, 2, 1, 1, 0, 0]。
解释：第一天 73 华氏度，第二天 74 华氏度，比 73 大，所以对于第一天，只要等一天就能等到一个更暖和的气温。后面的同理。
你已经对 Next Greater Number 类型问题有些敏感了，这个问题本质上也是找 Next Greater Number，只不过现在不是问你 Next Greater Number 是多少，而是问你当前距离 Next Greater Number 的距离而已。
相同类型的问题，相同的思路，直接调用单调栈的算法模板，稍作改动就可以啦，直接上代码把。

1
2
3
4
5
6
7
8
9
10
11
12

vector<int> dailyTemperatures(vector<int>& T) {
    vector<int> ans(T.size());
    stack<int> s; // 这里放元素索引，而不是元素
    for (int i = T.size() - 1; i >= 0; i--) {
        while (!s.empty() && T[s.top()] <= T[i]) {
            s.pop();
        }
        ans[i] = s.empty() ? 0 : (s.top() - i); // 得到索引间距
        s.push(i); // 加入索引，而不是元素
    }
    return ans;
}

单调栈讲解完毕。下面开始另一个重点：如何处理「循环数组」。
同样是 Next Greater Number，现在假设给你的数组是个环形的，如何处理？
给你一个数组 [2,1,2,4,3]，你返回数组 [4,2,4,-1,4]。拥有了环形属性，最后一个元素 3 绕了一圈后找到了比自己大的元素 4 。

首先，计算机的内存都是线性的，没有真正意义上的环形数组，但是我们可以模拟出环形数组的效果，一般是通过 % 运算符求模（余数），获得环形特效：

1
2
3
4
5
6

int[] arr = {1,2,3,4,5};
int n = arr.length, index = 0;
while (true) {
    print(arr[index % n]);
    index++;
}

回到 Next Greater Number 的问题，增加了环形属性后，问题的难点在于：这个 Next 的意义不仅仅是当前元素的右边了，有可能出现在当前元素的左边（如上例）。
明确问题，问题就已经解决了一半了。我们可以考虑这样的思路：将原始数组“翻倍”，就是在后面再接一个原始数组，这样的话，按照之前“比身高”的流程，每个元素不仅可以比较自己右边的元素，而且也可以和左边的元素比较了。

怎么实现呢？你当然可以把这个双倍长度的数组构造出来，然后套用算法模板。但是，我们可以不用构造新数组，而是利用循环数组的技巧来模拟。直接看代码吧：

1
2
3
4
5
6
7
8
9
10
11
12
13

vector<int> nextGreaterElements(vector<int>& nums) {
    int n = nums.size();
    vector<int> res(n); // 存放结果
    stack<int> s;
    // 假装这个数组长度翻倍了
    for (int i = 2 * n - 1; i >= 0; i--) {
        while (!s.empty() && s.top() <= nums[i % n])
            s.pop();
        res[i % n] = s.empty() ? -1 : s.top();
        s.push(nums[i % n]);
    }
    return res;
}

至此，你已经掌握了单调栈的设计方法及代码模板，学会了解决 Next Greater Number，并能够处理循环数组了。
你的在看，是对我的鼓励。关注公众号：labuladong

上一篇：二叉搜索树操作集锦
下一篇：特殊数据结构：单调队列
目录

特殊数据结构：单调队列

前文讲了一种特殊的数据结构「单调栈」monotonic stack，解决了一类问题「Next Greater Number」，本文写一个类似的数据结构「单调队列」。
也许这种数据结构的名字你没听过，其实没啥难的，就是一个「队列」，只是使用了一点巧妙的方法，使得队列中的元素单调递增（或递减）。这个数据结构有什么用？可以解决滑动窗口的一系列问题。
看一道 LeetCode 题目，难度 hard：

一、搭建解题框架

这道题不复杂，难点在于如何在 O(1) 时间算出每个「窗口」中的最大值，使得整个算法在线性时间完成。在之前我们探讨过类似的场景，得到一个结论：
在一堆数字中，已知最值，如果给这堆数添加一个数，那么比较一下就可以很快算出最值；但如果减少一个数，就不一定能很快得到最值了，而要遍历所有数重新找最值。
回到这道题的场景，每个窗口前进的时候，要添加一个数同时减少一个数，所以想在 O(1) 的时间得出新的最值，就需要「单调队列」这种特殊的数据结构来辅助了。
一个普通的队列一定有这两个操作：

1
2
3
4
5
6

class Queue {
    void push(int n);
    // 或 enqueue，在队尾加入元素 n
    void pop();
    // 或 dequeue，删除队头元素
}

一个「单调队列」的操作也差不多：

1
2
3
4
5
6
7
8

class MonotonicQueue {
    // 在队尾添加元素 n
    void push(int n);
    // 返回当前队列中的最大值
    int max();
    // 队头元素如果是 n，删除它
    void pop(int n);
}

当然，这几个 API 的实现方法肯定跟一般的 Queue 不一样，不过我们暂且不管，而且认为这几个操作的时间复杂度都是 O(1)，先把这道「滑动窗口」问题的解答框架搭出来：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

vector<int> maxSlidingWindow(vector<int>& nums, int k) {
    MonotonicQueue window;
    vector<int> res;
    for (int i = 0; i < nums.size(); i++) {
        if (i < k - 1) { //先把窗口的前 k - 1 填满
            window.push(nums[i]);
        } else { // 窗口开始向前滑动
            window.push(nums[i]);
            res.push_back(window.max());
            window.pop(nums[i - k + 1]);
            // nums[i - k + 1] 就是窗口最后的元素
        }
    }
    return res;
}

这个思路很简单，能理解吧？下面我们开始重头戏，单调队列的实现。

二、实现单调队列数据结构

首先我们要认识另一种数据结构：deque，即双端队列。很简单：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

class deque {
    // 在队头插入元素 n
    void push_front(int n);
    // 在队尾插入元素 n
    void push_back(int n);
    // 在队头删除元素
    void pop_front();
    // 在队尾删除元素
    void pop_back();
    // 返回队头元素
    int front();
    // 返回队尾元素
    int back();
}

而且，这些操作的复杂度都是 O(1)。这其实不是啥稀奇的数据结构，用链表作为底层结构的话，很容易实现这些功能。
「单调队列」的核心思路和「单调栈」类似。单调队列的 push 方法依然在队尾添加元素，但是要把前面比新元素小的元素都删掉：

1
2
3
4
5
6
7
8
9
10

class MonotonicQueue {
private:
    deque<int> data;
public:
    void push(int n) {
        while (!data.empty() && data.back() < n) 
            data.pop_back();
        data.push_back(n);
    }
};

你可以想象，加入数字的大小代表人的体重，把前面体重不足的都压扁了，直到遇到更大的量级才停住。

如果每个元素被加入时都这样操作，最终单调队列中的元素大小就会保持一个单调递减的顺序，因此我们的 max() API 可以可以这样写：

1
2
3

int max() {
    return data.front();
}

pop() API 在队头删除元素 n，也很好写：

1
2
3
4

void pop(int n) {
    if (!data.empty() && data.front() == n)
        data.pop_front();
}

之所以要判断 data.front() == n，是因为我们想删除的队头元素 n 可能已经被「压扁」了，这时候就不用删除了：

至此，单调队列设计完毕，看下完整的解题代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

class MonotonicQueue {
private:
    deque<int> data;
public:
    void push(int n) {
        while (!data.empty() && data.back() < n) 
            data.pop_back();
        data.push_back(n);
    }
    
    int max() { return data.front(); }
    
    void pop(int n) {
        if (!data.empty() && data.front() == n)
            data.pop_front();
    }
};
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
    MonotonicQueue window;
    vector<int> res;
    for (int i = 0; i < nums.size(); i++) {
        if (i < k - 1) { //先填满窗口的前 k - 1
            window.push(nums[i]);
        } else { // 窗口向前滑动
            window.push(nums[i]);
            res.push_back(window.max());
            window.pop(nums[i - k + 1]);
        }
    }
    return res;
}

三、算法复杂度分析
读者可能疑惑，push 操作中含有 while 循环，时间复杂度不是 O(1) 呀，那么本算法的时间复杂度应该不是线性时间吧？
单独看 push 操作的复杂度确实不是 O(1)，但是算法整体的复杂度依然是 O(N) 线性时间。要这样想，nums 中的每个元素最多被 push_back 和 pop_back 一次，没有任何多余操作，所以整体的复杂度还是 O(N)。
空间复杂度就很简单了，就是窗口的大小 O(k)。
四、最后总结
有的读者可能觉得「单调队列」和「优先级队列」比较像，实际上差别很大的。
单调队列在添加元素的时候靠删除元素保持队列的单调性，相当于抽取出某个函数中单调递增（或递减）的部分；而优先级队列（二叉堆）相当于自动排序，差别大了去了。
赶紧去拿下 LeetCode 第 239 道题吧～

上一篇：特殊数据结构：单调栈
下一篇：设计Twitter
目录

拆解复杂问题：实现计算器

我们最终要实现的计算器功能如下：

1、输入一个字符串，可以包含+ - * /、数字、括号以及空格，你的算法返回运算结构。
2、要符合运算法则，括号的优先级最高，先乘除后加减。
3、除号是整数除法，无论正负都向 0 取整（5/2=2，-5/2=-2）。
4、可以假定输入的算式一定合法，且计算过程不会出现整型溢出，不会出现除数为 0 的意外情况。
比如输入如下字符串，算法会返回 9：
3 * (2-6 /(3 -7))
可以看到，这就已经非常接近我们实际生活中使用的计算器了，虽然我们以前肯定都用过计算器，但是如果简单思考一下其算法实现，就会大惊失色：
1、按照常理处理括号，要先计算最内层的括号，然后向外慢慢化简。这个过程我们手算都容易出错，何况写成算法呢！
2、要做到先乘除，后加减，这一点教会小朋友还不算难，但教给计算机恐怕有点困难。
3、要处理空格。我们为了美观，习惯性在数字和运算符之间打个空格，但是计算之中得想办法忽略这些空格。
我记得很多大学数据结构的教材上，在讲栈这种数据结构的时候，应该都会用计算器举例，但是有一说一，讲的真的垃圾，不知道多少未来的计算机科学家就被这种简单的数据结构劝退了。
那么本文就来聊聊怎么实现上述一个功能完备的计算器功能，关键在于层层拆解问题，化整为零，逐个击破，相信这种思维方式能帮大家解决各种复杂问题。
下面就来拆解，从最简单的一个问题开始。

一、字符串转整数

是的，就是这么一个简单的问题，首先告诉我，怎么把一个字符串形式的正整数，转化成 int 型？

1
2
3
4
5
6
7

string s = "458";
int n = 0;
for (int i = 0; i < s.size(); i++) {
    char c = s[i];
    n = 10 * n + (c - '0');
}
// n 现在就等于 458

这个还是很简单的吧，老套路了。但是即便这么简单，依然有坑：**(c - '0')的这个括号不能省略，否则可能造成整型溢出**。
因为变量c是一个 ASCII 码，如果不加括号就会先加后减，想象一下s如果接近 INT_MAX，就会溢出。所以用括号保证先减后加才行。

二、处理加减法

现在进一步，如果输入的这个算式只包含加减法，而且不存在空格，你怎么计算结果？我们拿字符串算式1-12+3为例，来说一个很简单的思路：
1、先给第一个数字加一个默认符号+，变成+1-12+3。
2、把一个运算符和数字组合成一对儿，也就是三对儿+1，-12，+3，把它们转化成数字，然后放到一个栈中。
3、将栈中所有的数字求和，就是原算式的结果。
我们直接看代码，结合一张图就看明白了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

int calculate(string s) {
    stack<int> stk;
    // 记录算式中的数字
    int num = 0;
    // 记录 num 前的符号，初始化为 +
    char sign = '+';
    for (int i = 0; i < s.size(); i++) {
        char c = s[i];
        // 如果是数字，连续读取到 num
        if (isdigit(c)) 
            num = 10 * num + (c - '0');
        // 如果不是数字，就是遇到了下一个符号，
        // 之前的数字和符号就要存进栈中
        if (!isdigit(c) || i == s.size() - 1) {
            switch (sign) {
                case '+':
                    stk.push(num); break;
                case '-':
                    stk.push(-num); break;
            }
            // 更新符号为当前符号，数字清零
            sign = c;
            num = 0;
        }
    }
    // 将栈中所有结果求和就是答案
    int res = 0;
    while (!stk.empty()) {
        res += stk.top();
        stk.pop();
    }
    return res;
}

我估计就是中间带switch语句的部分有点不好理解吧，i就是从左到右扫描，sign和num跟在它身后。当s[i]遇到一个运算符时，情况是这样的：

所以说，此时要根据sign的 case 不同选择nums的正负号，存入栈中，然后更新sign并清零nums记录下一对儿符合和数字的组合。
另外注意，不只是遇到新的符号会触发入栈，当i走到了算式的尽头（i == s.size() - 1），也应该将前面的数字入栈，方便后续计算最终结果。

至此，仅处理紧凑加减法字符串的算法就完成了，请确保理解以上内容，后续的内容就基于这个框架修修改改就完事儿了。

三、处理乘除法

其实思路跟仅处理加减法没啥区别，拿字符串2-3*4+5举例，核心思路依然是把字符串分解成符号和数字的组合。
比如上述例子就可以分解为+2，-3，*4，+5几对儿，我们刚才不是没有处理乘除号吗，很简单，其他部分都不用变，在switch部分加上对应的 case 就行了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

for (int i = 0; i < s.size(); i++) {
    char c = s[i];
    if (isdigit(c)) 
        num = 10 * num + (c - '0');
    if (!isdigit(c) || i == s.size() - 1) {
        switch (sign) {
            int pre;
            case '+':
                stk.push(num); break;
            case '-':
                stk.push(-num); break;
            // 只要拿出前一个数字做对应运算即可
            case '*':
                pre = stk.top();
                stk.pop();
                stk.push(pre * num);
                break;
            case '/':
                pre = stk.top();
                stk.pop();
                stk.push(pre / num);
                break;
        }
        // 更新符号为当前符号，数字清零
        sign = c;
        num = 0;
    }
}

乘除法优先于加减法体现在，乘除法可以和栈顶的数结合，而加减法只能把自己放入栈。
现在我们思考一下如何处理字符串中可能出现的空格字符。其实也非常简单，想想空格字符的出现，会影响我们现有代码的哪一部分？

1
2
3
4
5
6

// 如果 c 非数字
if (!isdigit(c) || i == s.size() - 1) {
    switch (c) {...}
    sign = c;
    num = 0;
}

显然空格会进入这个 if 语句，但是我们并不想让空格的情况进入这个 if，因为这里会更新sign并清零nums，空格根本就不是运算符，应该被忽略。
那么只要多加一个条件即可：

1
2
3

if ((!isdigit(c) && c != ' ') || i == s.size() - 1) {
    ...
}

好了，现在我们的算法已经可以按照正确的法则计算加减乘除，并且自动忽略空格符，剩下的就是如何让算法正确识别括号了。

四、处理括号

处理算式中的括号看起来应该是最难的，但真没有看起来那么难。
为了规避编程语言的繁琐细节，我把前面解法的代码翻译成 Python 版本：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

def calculate(s: str) -> int:
        
    def helper(s: List) -> int:
        stack = []
        sign = '+'
        num = 0
        while len(s) > 0:
            c = s.pop(0)
            if c.isdigit():
                num = 10 * num + int(c)
            if (not c.isdigit() and c != ' ') or len(s) == 0:
                if sign == '+':
                    stack.append(num)
                elif sign == '-':
                    stack.append(-num)
                elif sign == '*':
                    stack[-1] = stack[-1] * num
                elif sign == '/':
                    # python 除法向 0 取整的写法
                    stack[-1] = int(stack[-1] / float(num))                    
                num = 0
                sign = c
        return sum(stack)
    # 需要把字符串转成列表方便操作
    return helper(list(s))

这段代码跟刚才 C++ 代码完全相同，唯一的区别是，不是从左到右遍历字符串，而是不断从左边pop出字符，本质还是一样的。
那么，为什么说处理括号没有看起来那么难呢，因为括号具有递归性质。我们拿字符串3*(4-5/2)-6举例：
calculate(3*(4-5/2)-6)
= 3 * calculate(4-5/2) - 6
= 3 * 2 - 6
= 0
可以脑补一下，无论多少层括号嵌套，通过 calculate 函数递归调用自己，都可以将括号中的算式化简成一个数字。换句话说，括号包含的算式，我们直接视为一个数字就行了。
现在的问题是，递归的开始条件和结束条件是什么？遇到(开始递归，遇到)结束递归：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

def calculate(s: str) -> int:
        
    def helper(s: List) -> int:
        stack = []
        sign = '+'
        num = 0
        while len(s) > 0:
            c = s.pop(0)
            if c.isdigit():
                num = 10 * num + int(c)
            # 遇到左括号开始递归计算 num
            if c == '(':
                num = helper(s)
            if (not c.isdigit() and c != ' ') or len(s) == 0:
                if sign == '+': ...
                elif sign == '-': ... 
                elif sign == '*': ...
                elif sign == '/': ...
                num = 0
                sign = c
            # 遇到右括号返回递归结果
            if c == ')': break
        return sum(stack)
    return helper(list(s))

你看，加了两三行代码，就可以处理括号了，这就是递归的魅力。至此，计算器的全部功能就实现了，通过对问题的层层拆解化整为零，再回头看，这个问题似乎也没那么复杂嘛。

五、最后总结

本文借实现计算器的问题，主要想表达的是一种处理复杂问题的思路。
我们首先从字符串转数字这个简单问题开始，进而处理只包含加减法的算式，进而处理包含加减乘除四则运算的算式，进而处理空格字符，进而处理包含括号的算式。
可见，对于一些比较困难的问题，其解法并不是一蹴而就的，而是步步推进，螺旋上升的。如果一开始给你原题，你不会做，甚至看不懂答案，都很正常，关键在于我们自己如何简化问题，如何以退为进。
退而求其次是一种很聪明策略。你想想啊，假设这是一道考试题，你不会实现这个计算器，但是你写了字符串转整数的算法并指出了容易溢出的陷阱，那起码可以得 20 分吧；如果你能够处理加减法，那可以得 40 分吧；如果你能处理加减乘除四则运算，那起码够 70 分了；再加上处理空格字符，80 有了吧。我就是不会处理括号，那就算了，80 已经很 OK 了好不好。

上一篇：常用的位操作
下一篇：烧饼排序
目录

数据结构系列

• 学习算法和刷题的思路指南
• 学习数据结构和算法读什么书
• 二叉堆详解实现优先级队列
• LRU算法详解
• 二叉搜索树操作集锦
• 特殊数据结构：单调栈
• 特殊数据结构：单调队列
• 设计Twitter
• 递归反转链表的一部分
• 队列实现栈|栈实现队列
  这一章主要是一些特殊的数据结构设计，比如单调栈解决 Next Greater Number，单调队列解决滑动窗口问题；还有常用数据结构的操作，比如链表、树、二叉堆。

设计Twitter

「design Twitter」是 LeetCode 上第 335 道题目，不仅题目本身很有意思，而且把合并多个有序链表的算法和面向对象设计（OO design）结合起来了，很有实际意义，本文就带大家来看看这道题。
至于 Twitter 的什么功能跟算法有关系，等我们描述一下题目要求就知道了。

一、题目及应用场景简介

Twitter 和微博功能差不多，我们主要要实现这样几个 API：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

class Twitter {
    /** user 发表一条 tweet 动态 */
    public void postTweet(int userId, int tweetId) {}
    
    /** 返回该 user 关注的人（包括他自己）最近的动态 id，
    最多 10 条，而且这些动态必须按从新到旧的时间线顺序排列。*/
    public List<Integer> getNewsFeed(int userId) {}
    
    /** follower 关注 followee，如果 Id 不存在则新建 */
    public void follow(int followerId, int followeeId) {}
    
    /** follower 取关 followee，如果 Id 不存在则什么都不做 */
    public void unfollow(int followerId, int followeeId) {}
}

举个具体的例子，方便大家理解 API 的具体用法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

Twitter twitter = new Twitter();
twitter.postTweet(1, 5);
// 用户 1 发送了一条新推文 5
twitter.getNewsFeed(1);
// return [5]，因为自己是关注自己的
twitter.follow(1, 2);
// 用户 1 关注了用户 2
twitter.postTweet(2, 6);
// 用户2发送了一个新推文 (id = 6)
twitter.getNewsFeed(1);
// return [6, 5]
// 解释：用户 1 关注了自己和用户 2，所以返回他们的最近推文
// 而且 6 必须在 5 之前，因为 6 是最近发送的
twitter.unfollow(1, 2);
// 用户 1 取消关注了用户 2
twitter.getNewsFeed(1);
// return [5]

这个场景在我们的现实生活中非常常见。拿朋友圈举例，比如我刚加到女神的微信，然后我去刷新一下我的朋友圈动态，那么女神的动态就会出现在我的动态列表，而且会和其他动态按时间排好序。只不过 Twitter 是单向关注，微信好友相当于双向关注。除非，被屏蔽…
这几个 API 中大部分都很好实现，最核心的功能难点应该是 getNewsFeed，因为返回的结果必须在时间上有序，但问题是用户的关注是动态变化的，怎么办？
这里就涉及到算法了：如果我们把每个用户各自的推文存储在链表里，每个链表节点存储文章 id 和一个时间戳 time（记录发帖时间以便比较），而且这个链表是按 time 有序的，那么如果某个用户关注了 k 个用户，我们就可以用合并 k 个有序链表的算法合并出有序的推文列表，正确地 getNewsFeed 了！
具体的算法等会讲解。不过，就算我们掌握了算法，应该如何编程表示用户 user 和推文动态 tweet 才能把算法流畅地用出来呢？这就涉及简单的面向对象设计了，下面我们来由浅入深，一步一步进行设计。

二、面向对象设计

根据刚才的分析，我们需要一个 User 类，储存 user 信息，还需要一个 Tweet 类，储存推文信息，并且要作为链表的节点。所以我们先搭建一下整体的框架：

1
2
3
4
5
6
7
8
9
10

class Twitter {
    private static int timestamp = 0;
    private static class Tweet {}
    private static class User {}
    /* 还有那几个 API 方法 */
    public void postTweet(int userId, int tweetId) {}
    public List<Integer> getNewsFeed(int userId) {}
    public void follow(int followerId, int followeeId) {}
    public void unfollow(int followerId, int followeeId) {}
}

之所以要把 Tweet 和 User 类放到 Twitter 类里面，是因为 Tweet 类必须要用到一个全局时间戳 timestamp，而 User 类又需要用到 Tweet 类记录用户发送的推文，所以它们都作为内部类。不过为了清晰和简洁，下文会把每个内部类和 API 方法单独拿出来实现。
1、Tweet 类的实现
根据前面的分析，Tweet 类很容易实现：每个 Tweet 实例需要记录自己的 tweetId 和发表时间 time，而且作为链表节点，要有一个指向下一个节点的 next 指针。

1
2
3
4
5
6
7
8
9
10
11

class Tweet {
    private int id;
    private int time;
    private Tweet next;
    // 需要传入推文内容（id）和发文时间
    public Tweet(int id, int time) {
        this.id = id;
        this.time = time;
        this.next = null;
    }
}

2、User 类的实现
我们根据实际场景想一想，一个用户需要存储的信息有 userId，关注列表，以及该用户发过的推文列表。其中关注列表应该用集合（Hash Set）这种数据结构来存，因为不能重复，而且需要快速查找；推文列表应该由链表这种数据结构储存，以便于进行有序合并的操作。画个图理解一下：

除此之外，根据面向对象的设计原则，「关注」「取关」和「发文」应该是 User 的行为，况且关注列表和推文列表也存储在 User 类中，所以我们也应该给 User 添加 follow，unfollow 和 post 这几个方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

// static int timestamp = 0
class User {
    private int id;
    public Set<Integer> followed;
    // 用户发表的推文链表头结点
    public Tweet head;
    public User(int userId) {
        followed = new HashSet<>();
        this.id = userId;
        this.head = null;
        // 关注一下自己
        follow(id);
    }
    public void follow(int userId) {
        followed.add(userId);
    }
    public void unfollow(int userId) {
        // 不可以取关自己
        if (userId != this.id)
            followed.remove(userId);
    }
    public void post(int tweetId) {
        Tweet twt = new Tweet(tweetId, timestamp);
        timestamp++;
        // 将新建的推文插入链表头
        // 越靠前的推文 time 值越大
        twt.next = head;
        head = twt;
    }
}

3、几个 API 方法的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

class Twitter {
    private static int timestamp = 0;
    private static class Tweet {...}
    private static class User {...}
    // 我们需要一个映射将 userId 和 User 对象对应起来
    private HashMap<Integer, User> userMap = new HashMap<>();
    /** user 发表一条 tweet 动态 */
    public void postTweet(int userId, int tweetId) {
        // 若 userId 不存在，则新建
        if (!userMap.containsKey(userId))
            userMap.put(userId, new User(userId));
        User u = userMap.get(userId);
        u.post(tweetId);
    }
    
    /** follower 关注 followee */
    public void follow(int followerId, int followeeId) {
        // 若 follower 不存在，则新建
		if(!userMap.containsKey(followerId)){
			User u = new User(followerId);
			userMap.put(followerId, u);
		}
        // 若 followee 不存在，则新建
		if(!userMap.containsKey(followeeId)){
			User u = new User(followeeId);
			userMap.put(followeeId, u);
		}
		userMap.get(followerId).follow(followeeId);
    }
    
    /** follower 取关 followee，如果 Id 不存在则什么都不做 */
    public void unfollow(int followerId, int followeeId) {
        if (userMap.containsKey(followerId)) {
            User flwer = userMap.get(followerId);
            flwer.unfollow(followeeId);
        }
    }
    /** 返回该 user 关注的人（包括他自己）最近的动态 id，
    最多 10 条，而且这些动态必须按从新到旧的时间线顺序排列。*/
    public List<Integer> getNewsFeed(int userId) {
        // 需要理解算法，见下文
    }
}

三、算法设计

实现合并 k 个有序链表的算法需要用到优先级队列（Priority Queue），这种数据结构是「二叉堆」最重要的应用，你可以理解为它可以对插入的元素自动排序。乱序的元素插入其中就被放到了正确的位置，可以按照从小到大（或从大到小）有序地取出元素。

1
2
3
4
5
6
7
8

PriorityQueue pq
# 乱序插入
for i in {2,4,1,9,6}:
    pq.add(i)
while pq not empty:
    # 每次取出第一个（最小）元素
    print(pq.pop())
# 输出有序：1,2,4,6,9

借助这种牛逼的数据结构支持，我们就很容易实现这个核心功能了。注意我们把优先级队列设为按 time 属性从大到小降序排列，因为 time 越大意味着时间越近，应该排在前面：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

public List<Integer> getNewsFeed(int userId) {
    List<Integer> res = new ArrayList<>();
    if (!userMap.containsKey(userId)) return res;
    // 关注列表的用户 Id
    Set<Integer> users = userMap.get(userId).followed;
    // 自动通过 time 属性从大到小排序，容量为 users 的大小
    PriorityQueue<Tweet> pq = 
        new PriorityQueue<>(users.size(), (a, b)->(b.time - a.time));
    // 先将所有链表头节点插入优先级队列
    for (int id : users) {
        Tweet twt = userMap.get(id).head;
        if (twt == null) continue;
        pq.add(twt);
    }
    while (!pq.isEmpty()) {
        // 最多返回 10 条就够了
        if (res.size() == 10) break;
        // 弹出 time 值最大的（最近发表的）
        Tweet twt = pq.poll();
        res.add(twt.id);
        // 将下一篇 Tweet 插入进行排序
        if (twt.next != null) 
            pq.add(twt.next);
    }
    return res;
}

这个过程是这样的，下面是我制作的一个 GIF 图描述合并链表的过程。假设有三个 Tweet 链表按 time 属性降序排列，我们把他们降序合并添加到 res 中。注意图中链表节点中的数字是 time 属性，不是 id 属性：

至此，这道一个极其简化的 Twitter 时间线功能就设计完毕了。

四、最后总结

本文运用简单的面向对象技巧和合并 k 个有序链表的算法设计了一套简化的时间线功能，这个功能其实广泛地运用在许多社交应用中。
我们先合理地设计出 User 和 Tweet 两个类，然后基于这个设计之上运用算法解决了最重要的一个功能。可见实际应用中的算法并不是孤立存在的，需要和其他知识混合运用，才能发挥实际价值。
当然，实际应用中的社交 App 数据量是巨大的，考虑到数据库的读写性能，我们的设计可能承受不住流量压力，还是有些太简化了。而且实际的应用都是一个极其庞大的工程，比如下图，是 Twitter 这样的社交网站大致的系统结构：

我们解决的问题应该只能算 Timeline Service 模块的一小部分，功能越多，系统的复杂性可能是指数级增长的。所以说合理的顶层设计十分重要，其作用是远超某一个算法的。
最后，Github 上有一个优秀的开源项目叫 system-design-primer，专门收集了很多大型系统设计的案例和解析，而且有中文版本，上面这个图也出自该项目。对系统设计感兴趣的读者可以点击链接查看。
PS：本文前两张图片和 GIF 是我第一次尝试用平板的绘图软件制作的，花了很多时间，尤其是 GIF 图，需要一帧一帧制作。如果本文内容对你有帮助，点个赞分个享，鼓励一下我呗！

上一篇：特殊数据结构：单调队列
下一篇：递归反转链表的一部分
目录