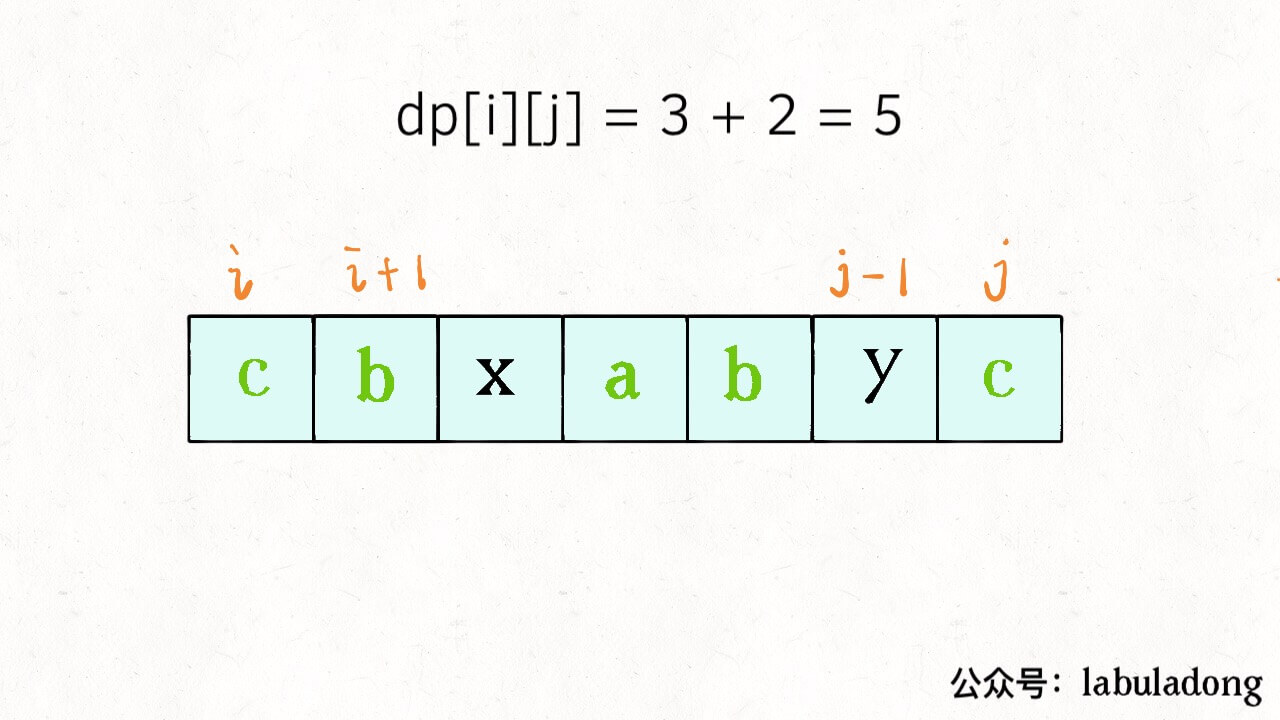
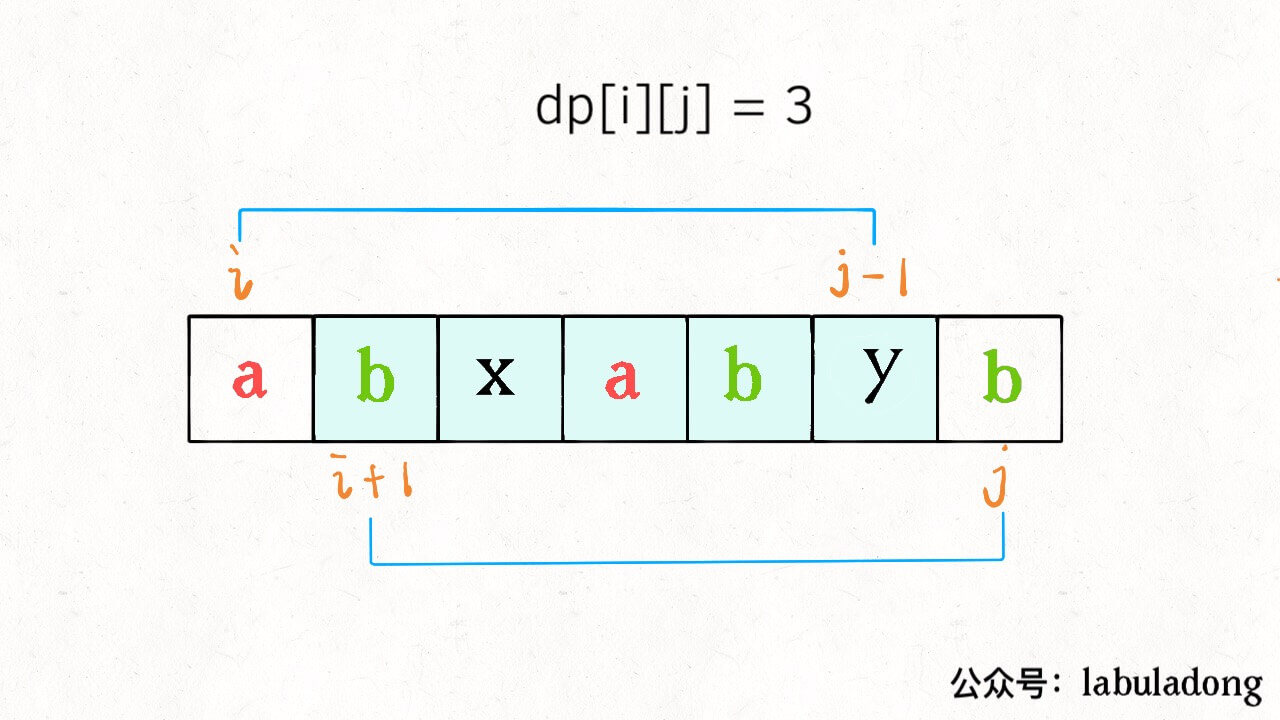
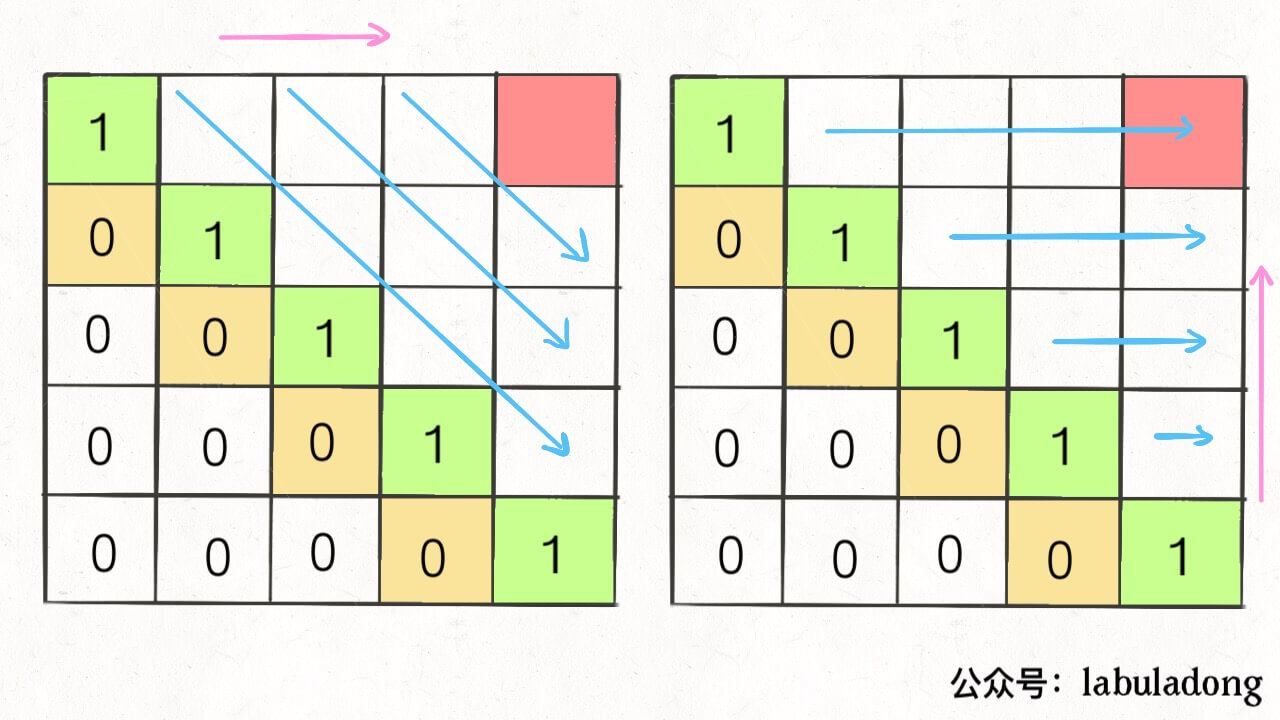
22Al的β衰变谱

摘要

我们在兰州RIBLL1上开展了一个Al22衰变实验，主束为28Si. 半衰期91ms被测定。βp，β2p，βα，βγ的测定使得我们得以更新能级纲图。通过Geant4的模拟，我们进一步精确测定分支比，并对部分质子峰结构特征得以解释。

介绍

在过去几十年里，原理稳定线的奇异核一直是核物理领域经久不衰的研究热点。原子核的诸多性质诸如同位旋、能级宽度等一系列物理量随着原子核向远离稳定线延申，产生了诸多奇异的效应。通过这些特性有助于我们深入研究原子核的结构信息和衰变机制。而在其中，通过β衰变谱来开展研究工作成为了滴线附近原子核结构信息和检验并完善壳模型理论的强有力的工具。
奇异核22Al是Al同位素中最缺中子的一个核素，有13个质子，9个中子，Tz为-2，结合能只有20keV. 1982年第一次被Cable观测到。在他的实验中，22Al通过24Mg(3He,p4n)的反应生成(110MeV)。Al原子通过He-jet技术被输运。在衰变谱中，仅仅高能区的两个峰(8212,8537keV)能够被观测到，低能区的部分由于其他核的污染，无法进行观测。 这两个峰被指认为从IAS态到Na21的基态和激发态。IAS态的激发能为13650keV。测定的半衰期为70ms。 由于实验条件的限制，没有确定绝对的分支比。随后，Cable在另一个实验中观测到了β2p衰变事件。在那个实验中，他观测到了两条beta2p衰变分支。基于能量的考虑，这两条分支归到Na20的基态和第一激发态。在最近的实验中，Blank测到了betaalpha衰变，通过将Al22注入到鬼探测器和气体探测器。测得的T1/2为59ms。精确的能级纲图以及实验分支比被测得。然而这个实验也受到了污染，在Ar36生成的次级束中，仅有30%的是Al22核素。那篇文章中还进行了壳模型计算。
尽管Al22这个核已经被研究了很久，但依旧有一些不确定和局限。 由于较强的污染，部分月前丢失或者被污染物中更强的分支掩盖。此外，先前的实验中也没有观测到γ射线。实验的目的是提高beta衰变的测量，通过不同的方式：更纯的22Al次级束，更高的统计，带电粒子测量更好的能量分辨，gamma探测器来辅助指认跃迁。

实验技术

实验于2017年11月在兰州RIBLL1上开展。主束为74.27MeV/u，80enA的28Si14+，通过K69 Sector Focus Cyclotron和K450 Separate Sector Cyclotron 。次级束通过将28Si打到1581um厚的Be9靶上。RIBLL1的主要设置为筛选Al22做了优化。Al22的束流强度和纯度分别为（）和（）。次级束粒子通过ΔE和TOF来筛选想要的粒子。通过位于T1、T2的闪烁薄膜探测器给出的飞行时间（TOF）结合位于T2的QSDΔE1和QSDΔE2给出的能损信号（ΔE）可以建立ΔE–TOF图谱鉴别束流粒子，双重ΔE探测器的能量和时间信号都可以用于进一步提高对束流重离子的鉴别能力。本实验研究的核为Na20，Mg21，Al22，Si23.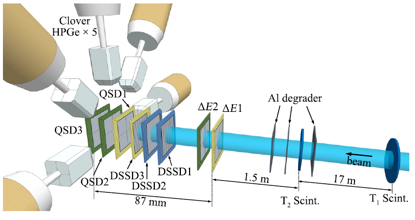

探测器阵列主要由三块双面硅条探测器（DSSD）、五块四分硅探测器（QSD）及外部五个Clover型的高纯锗探测器组成。经过上游铝降能片降能后的束流具有一定能散，目标核的射程分布在三块DSSD，即DSSD做停阻束流中目标核的注入探测器，并对注入核的衰变带电粒子进行测量，硅探测器对从内部发射的带电粒子具有极高的探测效率。每个DSSD x–y像素格都可视为独立探测器，这样在连续束、高束流注入率的条件下各单个像素格内仍能保持较低注入率，衰变事件和注入事件的时间关联仍然可以建立。三块DSSD的厚度分别为142um，40um，304um。Al22主要分布在后两块Si，QSD1用于探测DSSD中感兴趣核衰变产生的β粒子，QSD2和QSD3位于束流最下游，用于测量束流中的轻粒子（1H、2H、3H、4He等），反符合去掉穿透DSSD的轻粒子在DSSD中的能损信号。DSSD被五个clover环绕，下侧有三个LaBr3探测器，用来测量γ射线。

分析及结果

能量刻度及注入深度分布

重离子能量刻度通过将实验中任意两块DSSD组成的望远镜谱与LISE计算的望远镜谱做对照，调整刻度参数，使实验谱的中心与计算的de-E线基本重合；随后通过应用LISE计算得到的能量射程拟合函数计算注入重离子的注入深度。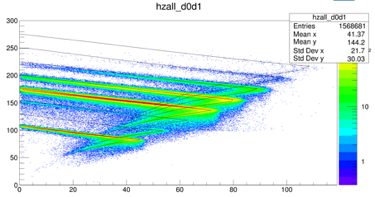

质子能量刻度应用文献中给出的质子峰数据。采用了※，※，※，※，※几个峰参与能量刻度。（考虑了弹道亏损效应。）和（β叠加效应）。

质子探测效率模拟

我们采用了Geant4工具包来模拟计算质子探测效率。质子的注入深度以及x-y平面分布采用了实验数据，在Si内各向同性发射。我们每隔0.5MeV的能量发射100000个质子，绘制了E-Eff曲线。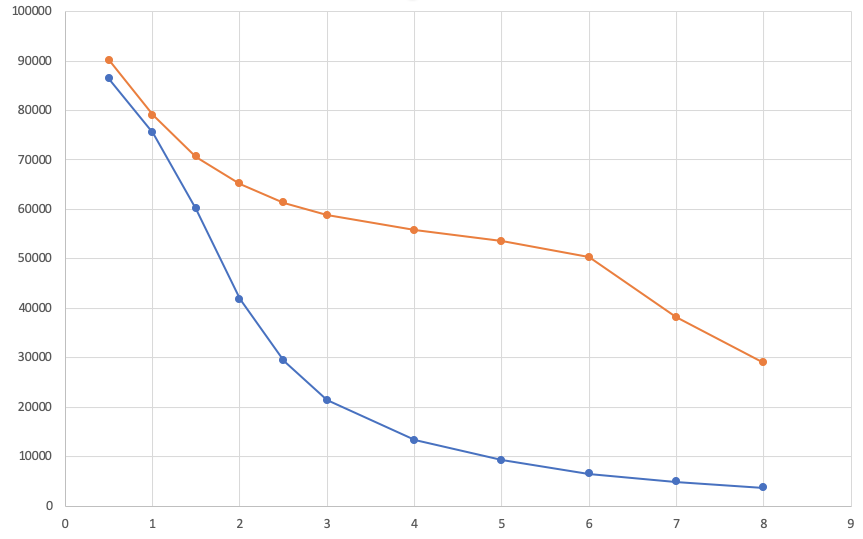

其中蓝线为40umSi的探测效率曲线，橙线为304umSi的探测效率曲线。

质子谱

这是最后一块Si的质子谱，其中蓝线未加入veto条件限制，而红线加入了veto条件限制。

这是中间一块Si的质子谱。

Geant4模拟质子谱

随后，我们应用EPJA2006文章中给出的质子能量分支比数据作为Geant4模拟输入，来研究β叠加效应。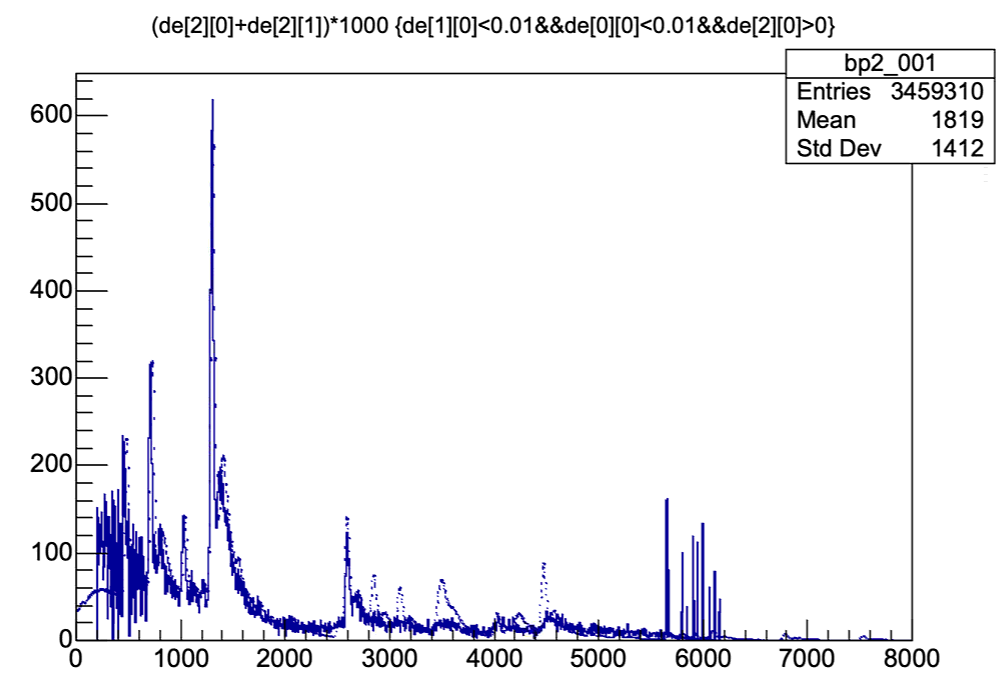

上图中实线为实验谱，虚线为经过归一之后的模拟谱。其中实验谱和模拟谱均未设置veto条件。

hexo发布网站到Github之后，可以直接通过访问Git个人主页。但hexo d部署的方式并不包含博客的源码，对于博客的迁移、更新、维护、多终端编辑并不友好。
在网上看到诸多同时管理hexo博客源文件和发布版本的教程，看似很优雅，但分支的切换、管理比较繁琐，同时一个严重的问题是，源代码的权限想要设为私有，而发布版本为公有。因而决定重新建立一个repo来管理源代码项目。

搭建Hexo环境

访问Hexo主页

title: 动态规划之博弈问题
author: 远方
tags:

• LeetCode
• 算法
  categories:
• LeetCode破局攻略
  date: 2016-01-01 19:20:00

动态规划之博弈问题

上一篇文章 几道智力题 中讨论到一个有趣的「石头游戏」，通过题目的限制条件，这个游戏是先手必胜的。但是智力题终究是智力题，真正的算法问题肯定不会是投机取巧能搞定的。所以，本文就借石头游戏来讲讲「假设两个人都足够聪明，最后谁会获胜」这一类问题该如何用动态规划算法解决。
博弈类问题的套路都差不多，下文举例讲解，其核心思路是在二维 dp 的基础上使用元组分别存储两个人的博弈结果。掌握了这个技巧以后，别人再问你什么俩海盗分宝石，俩人拿硬币的问题，你就告诉别人：我懒得想，直接给你写个算法算一下得了。
我们「石头游戏」改的更具有一般性：
你和你的朋友面前有一排石头堆，用一个数组 piles 表示，piles[i] 表示第 i 堆石子有多少个。你们轮流拿石头，一次拿一堆，但是只能拿走最左边或者最右边的石头堆。所有石头被拿完后，谁拥有的石头多，谁获胜。
石头的堆数可以是任意正整数，石头的总数也可以是任意正整数，这样就能打破先手必胜的局面了。比如有三堆石头 piles = [1, 100, 3]，先手不管拿 1 还是 3，能够决定胜负的 100 都会被后手拿走，后手会获胜。
假设两人都很聪明，请你设计一个算法，返回先手和后手的最后得分（石头总数）之差。比如上面那个例子，先手能获得 4 分，后手会获得 100 分，你的算法应该返回 -96。
这样推广之后，这个问题算是一道 Hard 的动态规划问题了。博弈问题的难点在于，两个人要轮流进行选择，而且都贼精明，应该如何编程表示这个过程呢？
还是强调多次的套路，首先明确 dp 数组的含义，然后和股票买卖系列问题类似，只要找到「状态」和「选择」，一切就水到渠成了。

一、定义 dp 数组的含义

定义 dp 数组的含义是很有技术含量的，同一问题可能有多种定义方法，不同的定义会引出不同的状态转移方程，不过只要逻辑没有问题，最终都能得到相同的答案。
我建议不要迷恋那些看起来很牛逼，代码很短小的奇技淫巧，最好是稳一点，采取可解释性最好，最容易推广的设计思路。本文就给出一种博弈问题的通用设计框架。
介绍 dp 数组的含义之前，我们先看一下 dp 数组最终的样子：

下文讲解时，认为元组是包含 first 和 second 属性的一个类，而且为了节省篇幅，将这两个属性简写为 fir 和 sec。比如按上图的数据，我们说 dp[1][3].fir = 10，dp[0][1].sec = 3。
先回答几个读者可能提出的问题：
这个二维 dp table 中存储的是元组，怎么编程表示呢？这个 dp table 有一半根本没用上，怎么优化？很简单，都不要管，先把解题的思路想明白了再谈也不迟。
以下是对 dp 数组含义的解释：

1
2
3
4
5

dp[i][j].fir 表示，对于 piles[i...j] 这部分石头堆，先手能获得的最高分数。
dp[i][j].sec 表示，对于 piles[i...j] 这部分石头堆，后手能获得的最高分数。
举例理解一下，假设 piles = [3, 9, 1, 2]，索引从 0 开始
dp[0][1].fir = 9 意味着：面对石头堆 [3, 9]，先手最终能够获得 9 分。
dp[1][3].sec = 2 意味着：面对石头堆 [9, 1, 2]，后手最终能够获得 2 分。

我们想求的答案是先手和后手最终分数之差，按照这个定义也就是 $dp[0][n-1].fir - dp[0][n-1].sec$，即面对整个 piles，先手的最优得分和后手的最优得分之差。

二、状态转移方程

写状态转移方程很简单，首先要找到所有「状态」和每个状态可以做的「选择」，然后择优。
根据前面对 dp 数组的定义，状态显然有三个：开始的索引 i，结束的索引 j，当前轮到的人。

1
2
3
4

dp[i][j][fir or sec]
其中：
0 <= i < piles.length
i <= j < piles.length

对于这个问题的每个状态，可以做的选择有两个：选择最左边的那堆石头，或者选择最右边的那堆石头。 我们可以这样穷举所有状态：

1
2
3
4
5

n = piles.length
for 0 <= i < n:
    for j <= i < n:
        for who in {fir, sec}:
            dp[i][j][who] = max(left, right)

上面的伪码是动态规划的一个大致的框架，股票系列问题中也有类似的伪码。这道题的难点在于，两人是交替进行选择的，也就是说先手的选择会对后手有影响，这怎么表达出来呢？
根据我们对 dp 数组的定义，很容易解决这个难点，写出状态转移方程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

dp[i][j].fir = max(piles[i] + dp[i+1][j].sec, piles[j] + dp[i][j-1].sec)
dp[i][j].fir = max(    选择最左边的石头堆     ,     选择最右边的石头堆     )
# 解释：我作为先手，面对 piles[i...j] 时，有两种选择：
# 要么我选择最左边的那一堆石头，然后面对 piles[i+1...j]
# 但是此时轮到对方，相当于我变成了后手；
# 要么我选择最右边的那一堆石头，然后面对 piles[i...j-1]
# 但是此时轮到对方，相当于我变成了后手。
if 先手选择左边:
    dp[i][j].sec = dp[i+1][j].fir
if 先手选择右边:
    dp[i][j].sec = dp[i][j-1].fir
# 解释：我作为后手，要等先手先选择，有两种情况：
# 如果先手选择了最左边那堆，给我剩下了 piles[i+1...j]
# 此时轮到我，我变成了先手；
# 如果先手选择了最右边那堆，给我剩下了 piles[i...j-1]
# 此时轮到我，我变成了先手。

根据 dp 数组的定义，我们也可以找出 base case，也就是最简单的情况：

1
2
3
4
5
6

dp[i][j].fir = piles[i]
dp[i][j].sec = 0
其中 0 <= i == j < n
# 解释：i 和 j 相等就是说面前只有一堆石头 piles[i]
# 那么显然先手的得分为 piles[i]
# 后手没有石头拿了，得分为 0

这里需要注意一点，我们发现 base case 是斜着的，而且我们推算 dp[i][j] 时需要用到 dp[i+1][j] 和 dp[i][j-1]：

所以说算法不能简单的一行一行遍历 dp 数组，而要斜着遍历数组：

说实话，斜着遍历二维数组说起来容易，你还真不一定能想出来怎么实现，不信你思考一下？这么巧妙的状态转移方程都列出来了，要是不会写代码实现，那真的很尴尬了。

三、代码实现

如何实现这个 fir 和 sec 元组呢，你可以用 python，自带元组类型；或者使用 C++ 的 pair 容器；或者用一个三维数组 dp[n][n][2]，最后一个维度就相当于元组；或者我们自己写一个 Pair 类：

1
2
3
4
5
6
7

class Pair {
    int fir, sec;
    Pair(int fir, int sec) {
        this.fir = fir;
        this.sec = sec;
    }
}

然后直接把我们的状态转移方程翻译成代码即可，可以注意一下斜着遍历数组的技巧：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

/* 返回游戏最后先手和后手的得分之差 */
int stoneGame(int[] piles) {
    int n = piles.length;
    // 初始化 dp 数组
    Pair[][] dp = new Pair[n][n];
    for (int i = 0; i < n; i++) 
        for (int j = i; j < n; j++)
            dp[i][j] = new Pair(0, 0);
    // 填入 base case
    for (int i = 0; i < n; i++) {
        dp[i][i].fir = piles[i];
        dp[i][i].sec = 0;
    }
    // 斜着遍历数组
    for (int l = 2; l <= n; l++) {
        for (int i = 0; i <= n - l; i++) {
            int j = l + i - 1;
            // 先手选择最左边或最右边的分数
            int left = piles[i] + dp[i+1][j].sec;
            int right = piles[j] + dp[i][j-1].sec;
            // 套用状态转移方程
            if (left > right) {
                dp[i][j].fir = left;
                dp[i][j].sec = dp[i+1][j].fir;
            } else {
                dp[i][j].fir = right;
                dp[i][j].sec = dp[i][j-1].fir;
            }
        }
    }
    Pair res = dp[0][n-1];
    return res.fir - res.sec;
}

动态规划解法，如果没有状态转移方程指导，绝对是一头雾水，但是根据前面的详细解释，读者应该可以清晰理解这一大段代码的含义。
而且，注意到计算 dp[i][j] 只依赖其左边和下边的元素，所以说肯定有优化空间，转换成一维 dp，想象一下把二维平面压扁，也就是投影到一维。但是，一维 dp 比较复杂，可解释性很差，大家就不必浪费这个时间去理解了。

四、最后总结

本文给出了解决博弈问题的动态规划解法。博弈问题的前提一般都是在两个聪明人之间进行，编程描述这种游戏的一般方法是二维 dp 数组，数组中通过元组分别表示两人的最优决策。
之所以这样设计，是因为先手在做出选择之后，就成了后手，后手在对方做完选择后，就变成了先手。这种角色转换使得我们可以重用之前的结果，典型的动态规划标志。
读到这里的朋友应该能理解算法解决博弈问题的套路了。学习算法，一定要注重算法的模板框架，而不是一些看起来牛逼的思路，也不要奢求上来就写一个最优的解法。不要舍不得多用空间，不要过早尝试优化，不要惧怕多维数组。dp 数组就是存储信息避免重复计算的，随便用，直到咱满意为止。
希望本文对你有帮助。

上一篇：动态规划之子序列问题解题模板
下一篇：贪心算法之区间调度问题
目录

title: 动态规划之四键键盘
author: 远方
tags:

• LeetCode
• 算法
  categories:
• LeetCode破局攻略
  date: 2016-01-01 19:20:00

动态规划之四键键盘

四键键盘问题很有意思，而且可以明显感受到：对 dp 数组的不同定义需要完全不同的逻辑，从而产生完全不同的解法。
首先看一下题目：

如何在 N 次敲击按钮后得到最多的 A？我们穷举呗，每次有对于每次按键，我们可以穷举四种可能，很明显就是一个动态规划问题。

第一种思路

这种思路会很容易理解，但是效率并不高，我们直接走流程：对于动态规划问题，首先要明白有哪些「状态」，有哪些「选择」。
具体到这个问题，对于每次敲击按键，有哪些「选择」是很明显的：4 种，就是题目中提到的四个按键，分别是 A、C-A、C-C、C-V（Ctrl 简写为 C）。
接下来，思考一下对于这个问题有哪些「状态」？或者换句话说，我们需要知道什么信息，才能将原问题分解为规模更小的子问题？
你看我这样定义三个状态行不行：第一个状态是剩余的按键次数，用 n 表示；第二个状态是当前屏幕上字符 A 的数量，用 a_num 表示；第三个状态是剪切板中字符 A 的数量，用 copy 表示。
如此定义「状态」，就可以知道 base case：当剩余次数 n 为 0 时，a_num 就是我们想要的答案。
结合刚才说的 4 种「选择」，我们可以把这几种选择通过状态转移表示出来：

1
2
3
4
5
6
7
8
9
10

dp(n - 1, a_num + 1, copy),    # A
解释：按下 A 键，屏幕上加一个字符
同时消耗 1 个操作数
dp(n - 1, a_num + copy, copy), # C-V
解释：按下 C-V 粘贴，剪切板中的字符加入屏幕
同时消耗 1 个操作数
dp(n - 2, a_num, a_num)        # C-A C-C
解释：全选和复制必然是联合使用的，
剪切板中 A 的数量变为屏幕上 A 的数量
同时消耗 2 个操作数

这样可以看到问题的规模 n 在不断减小，肯定可以到达 n = 0 的 base case，所以这个思路是正确的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

def maxA(N: int) -> int:
    # 对于 (n, a_num, copy) 这个状态，
    # 屏幕上能最终最多能有 dp(n, a_num, copy) 个 A
    def dp(n, a_num, copy):
        # base case
        if n <= 0: return a_num;
        # 几种选择全试一遍，选择最大的结果
        return max(
                dp(n - 1, a_num + 1, copy),    # A
                dp(n - 1, a_num + copy, copy), # C-V
                dp(n - 2, a_num, a_num)        # C-A C-C
            )
    # 可以按 N 次按键，屏幕和剪切板里都还没有 A
    return dp(N, 0, 0)

这个解法应该很好理解，因为语义明确。下面就继续走流程，用备忘录消除一下重叠子问题：

1
2
3
4
5
6
7
8
9
10
11
12
13

def maxA(N: int) -> int:
    # 备忘录
    memo = dict()
    def dp(n, a_num, copy):
        if n <= 0: return a_num;
        # 避免计算重叠子问题
        if (n, a_num, copy) in memo:
            return memo[(n, a_num, copy)]
        memo[(n, a_num, copy)] = max(
                # 几种选择还是一样的
            )
        return memo[(n, a_num, copy)]
    return dp(N, 0, 0)

这样优化代码之后，子问题虽然没有重复了，但数目仍然很多，在 LeetCode 提交会超时的。
我们尝试分析一下这个算法的时间复杂度，就会发现不容易分析。我们可以把这个 dp 函数写成 dp 数组：

1
2

dp[n][a_num][copy]
# 状态的总数（时空复杂度）就是这个三维数组的体积

我们知道变量 n 最多为 N，但是 a_num 和 copy 最多为多少我们很难计算，复杂度起码也有 O(N^3) 把。所以这个算法并不好，复杂度太高，且已经无法优化了。
这也就说明，我们这样定义「状态」是不太优秀的，下面我们换一种定义 dp 的思路。

第二种思路

这种思路稍微有点复杂，但是效率高。继续走流程，「选择」还是那 4 个，但是这次我们只定义一个「状态」，也就是剩余的敲击次数 n。
这个算法基于这样一个事实，最优按键序列一定只有两种情况：
要么一直按 A：A,A,…A（当 N 比较小时）。
要么是这么一个形式：A,A,…C-A,C-C,C-V,C-V,…C-V（当 N 比较大时）。
因为字符数量少（N 比较小）时，C-A C-C C-V 这一套操作的代价相对比较高，可能不如一个个按 A；而当 N 比较大时，后期 C-V 的收获肯定很大。这种情况下整个操作序列大致是：开头连按几个 A，然后 C-A C-C 组合再接若干 C-V，然后再 C-A C-C 接着若干 C-V，循环下去。
换句话说，最后一次按键要么是 A 要么是 C-V。明确了这一点，可以通过这两种情况来设计算法：

1
2
3
4
5
6
7

int[] dp = new int[N + 1];
// 定义：dp[i] 表示 i 次操作后最多能显示多少个 A
for (int i = 0; i <= N; i++) 
    dp[i] = max(
            这次按 A 键，
            这次按 C-V
        )

对于「按 A 键」这种情况，就是状态 i - 1 的屏幕上新增了一个 A 而已，很容易得到结果：

1
2

// 按 A 键，就比上次多一个 A 而已
dp[i] = dp[i - 1] + 1;

但是，如果要按 C-V，还要考虑之前是在哪里 C-A C-C 的。
刚才说了，最优的操作序列一定是 C-A C-C 接着若干 C-V，所以我们用一个变量 j 作为若干 C-V 的起点。那么 j 之前的 2 个操作就应该是 C-A C-C 了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

public int maxA(int N) {
    int[] dp = new int[N + 1];
    dp[0] = 0;
    for (int i = 1; i <= N; i++) {
        // 按 A 键
        dp[i] = dp[i - 1] + 1;
        for (int j = 2; j < i; j++) {
            // 全选 & 复制 dp[j-2]，连续粘贴 i - j 次
            // 屏幕上共 dp[j - 2] * (i - j + 1) 个 A
            dp[i] = Math.max(dp[i], dp[j - 2] * (i - j + 1));
        }
    }
    // N 次按键之后最多有几个 A？
    return dp[N];
}

其中 j 变量减 2 是给 C-A C-C 留下操作数，看个图就明白了：

这样，此算法就完成了，时间复杂度 O(N^2)，空间复杂度 O(N)，这种解法应该是比较高效的了。

最后总结

动态规划难就难在寻找状态转移，不同的定义可以产生不同的状态转移逻辑，虽然最后都能得到正确的结果，但是效率可能有巨大的差异。
回顾第一种解法，重叠子问题已经消除了，但是效率还是低，到底低在哪里呢？抽象出递归框架：

1
2
3
4

def dp(n, a_num, copy):
    dp(n - 1, a_num + 1, copy),    # A
    dp(n - 1, a_num + copy, copy), # C-V
    dp(n - 2, a_num, a_num)        # C-A C-C

看这个穷举逻辑，是有可能出现这样的操作序列 C-A C-C，C-A C-C... 或者 C-V,C-V,...。然这种操作序列的结果不是最优的，但是我们并没有想办法规避这些情况的发生，从而增加了很多没必要的子问题计算。
回顾第二种解法，我们稍加思考就能想到，最优的序列应该是这种形式：A,A..C-A,C-C,C-V,C-V..C-A,C-C,C-V..。
根据这个事实，我们重新定义了状态，重新寻找了状态转移，从逻辑上减少了无效的子问题个数，从而提高了算法的效率。

上一篇：团灭 LeetCode 打家劫舍问题
下一篇：动态规划之正则表达
目录

title: 动态规划之正则表达
author: 远方
tags:

• LeetCode
• 算法
  categories:
• LeetCode破局攻略
  date: 2016-01-01 19:20:00

动态规划之正则表达

之前的文章「动态规划详解」收到了普遍的好评，今天写一个动态规划的实际应用：正则表达式。如果有读者对「动态规划」还不了解，建议先看一下上面那篇文章。
正则表达式匹配是一个很精妙的算法，而且难度也不小。本文主要写两个正则符号的算法实现：点号「.」和星号「*」，如果你用过正则表达式，应该明白他们的用法，不明白也没关系，等会会介绍。文章的最后，介绍了一种快速看出重叠子问题的技巧。
本文还有一个重要目的，就是教会读者如何设计算法。我们平时看别人的解法，直接看到一个面面俱到的完整答案，总觉得无法理解，以至觉得问题太难，自己太菜。我力求向读者展示，算法的设计是一个螺旋上升、逐步求精的过程，绝不是一步到位就能写出正确算法。本文会带你解决这个较为复杂的问题，让你明白如何化繁为简，逐个击破，从最简单的框架搭建出最终的答案。
前文无数次强调的框架思维，就是在这种设计过程中逐步培养的。下面进入正题，首先看一下题目：

一、热身

第一步，我们暂时不管正则符号，如果是两个普通的字符串进行比较，如何进行匹配？我想这个算法应该谁都会写：

1
2
3
4
5
6
7
8
9

bool isMatch(string text, string pattern) {
    if (text.size() != pattern.size()) 
        return false;
    for (int j = 0; j < pattern.size(); j++) {
        if (pattern[j] != text[j])
            return false;
    }
    return true;
}

然后，我稍微改造一下上面的代码，略微复杂了一点，但意思还是一样的，很容易理解吧：

1
2
3
4
5
6
7
8
9
10
11
12

bool isMatch(string text, string pattern) {
    int i = 0; // text 的索引位置
    int j = 0; // pattern 的索引位置
    while (j < pattern.size()) {
        if (i >= text.size()) 
            return false;
        if (pattern[j++] != text[i++])
            return false;
    }
    // 相等则说明完成匹配
    return j == text.size();
}

如上改写，是为了将这个算法改造成递归算法（伪码）：

1
2
3
4

def isMatch(text, pattern) -> bool:
    if pattern is empty: return (text is empty?)
    first_match = (text not empty) and pattern[0] == text[0]
    return first_match and isMatch(text[1:], pattern[1:])

如果你能够理解这段代码，恭喜你，你的递归思想已经到位，正则表达式算法虽然有点复杂，其实是基于这段递归代码逐步改造而成的。

二、处理点号「.」通配符

点号可以匹配任意一个字符，万金油嘛，其实是最简单的，稍加改造即可：

1
2
3
4

def isMatch(text, pattern) -> bool:
    if not pattern: return not text
    first_match = bool(text) and pattern[0] in {text[0], '.'}
    return first_match and isMatch(text[1:], pattern[1:])

三、处理「*」通配符

星号通配符可以让前一个字符重复任意次数，包括零次。那到底是重复几次呢？这似乎有点困难，不过不要着急，我们起码可以把框架的搭建再进一步：

1
2
3
4
5
6
7

def isMatch(text, pattern) -> bool:
    if not pattern: return not text
    first_match = bool(text) and pattern[0] in {text[0], '.'}
    if len(pattern) >= 2 and pattern[1] == '*':
        # 发现 '*' 通配符
    else:
        return first_match and isMatch(text[1:], pattern[1:])

星号前面的那个字符到底要重复几次呢？这需要计算机暴力穷举来算，假设重复 N 次吧。前文多次强调过，写递归的技巧是管好当下，之后的事抛给递归。具体到这里，不管 N 是多少，当前的选择只有两个：匹配 0 次、匹配 1 次。所以可以这样处理：

1
2
3
4
5
6

if len(pattern) >= 2 and pattern[1] == '*':
    return isMatch(text, pattern[2:]) or \
            first_match and isMatch(text[1:], pattern)
# 解释：如果发现有字符和 '*' 结合，
    # 或者匹配该字符 0 次，然后跳过该字符和 '*'
    # 或者当 pattern[0] 和 text[0] 匹配后，移动 text

可以看到，我们是通过保留 pattern 中的「*」，同时向后推移 text，来实现「*」将字符重复匹配多次的功能。举个简单的例子就能理解这个逻辑了。假设 pattern = a*, text = aaa，画个图看看匹配过程：

至此，正则表达式算法就基本完成了，

四、动态规划

我选择使用「备忘录」递归的方法来降低复杂度。有了暴力解法，优化的过程及其简单，就是使用两个变量 i, j 记录当前匹配到的位置，从而避免使用子字符串切片，并且将 i, j 存入备忘录，避免重复计算即可。
我将暴力解法和优化解法放在一起，方便你对比，你可以发现优化解法无非就是把暴力解法「翻译」了一遍，加了个 memo 作为备忘录，仅此而已。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# 带备忘录的递归
def isMatch(text, pattern) -> bool:
    memo = dict() # 备忘录
    def dp(i, j):
        if (i, j) in memo: return memo[(i, j)]
        if j == len(pattern): return i == len(text)
        first = i < len(text) and pattern[j] in {text[i], '.'}
        
        if j <= len(pattern) - 2 and pattern[j + 1] == '*':
            ans = dp(i, j + 2) or \
                    first and dp(i + 1, j)
        else:
            ans = first and dp(i + 1, j + 1)
            
        memo[(i, j)] = ans
        return ans
    
    return dp(0, 0)
# 暴力递归
def isMatch(text, pattern) -> bool:
    if not pattern: return not text
    first = bool(text) and pattern[0] in {text[0], '.'}
    if len(pattern) >= 2 and pattern[1] == '*':
        return isMatch(text, pattern[2:]) or \
                first and isMatch(text[1:], pattern)
    else:
        return first and isMatch(text[1:], pattern[1:])

有的读者也许会问，你怎么知道这个问题是个动态规划问题呢，你怎么知道它就存在「重叠子问题」呢，这似乎不容易看出来呀？
解答这个问题，最直观的应该是随便假设一个输入，然后画递归树，肯定是可以发现相同节点的。这属于定量分析，其实不用这么麻烦，下面我来教你定性分析，一眼就能看出「重叠子问题」性质。
先拿最简单的斐波那契数列举例，我们抽象出递归算法的框架：

1
2
3

def fib(n):
    fib(n - 1) #1
    fib(n - 2) #2

看着这个框架，请问原问题 f(n) 如何触达子问题 f(n - 2) ？有两种路径，一是 f(n) -> #1 -> #1, 二是 f(n) -> #2。前者经过两次递归，后者进过一次递归而已。两条不同的计算路径都到达了同一个问题，这就是「重叠子问题」，而且可以肯定的是，只要你发现一条重复路径，这样的重复路径一定存在千万条，意味着巨量子问题重叠。
同理，对于本问题，我们依然先抽象出算法框架：

1
2
3
4

def dp(i, j):
    dp(i, j + 2)     #1
    dp(i + 1, j)     #2
    dp(i + 1, j + 1) #3

提出类似的问题，请问如何从原问题 dp(i, j) 触达子问题 dp(i + 2, j + 2) ？至少有两种路径，一是 dp(i, j) -> #3 -> #3，二是 dp(i, j) -> #1 -> #2 -> #2。因此，本问题一定存在重叠子问题，一定需要动态规划的优化技巧来处理。

五、最后总结

通过本文，你深入理解了正则表达式的两种常用通配符的算法实现。其实点号「.」的实现及其简单，关键是星号「*」的实现需要用到动态规划技巧，稍微复杂些，但是也架不住我们对问题的层层拆解，逐个击破。另外，你掌握了一种快速分析「重叠子问题」性质的技巧，可以快速判断一个问题是否可以使用动态规划套路解决。
回顾整个解题过程，你应该能够体会到算法设计的流程：从简单的类似问题入手，给基本的框架逐渐组装新的逻辑，最终成为一个比较复杂、精巧的算法。所以说，读者不必畏惧一些比较复杂的算法问题，多思考多类比，再高大上的算法在你眼里也不过一个脆皮。

上一篇：动态规划之四键键盘
下一篇：最长公共子序列
目录

title: 动态规划系列
author: 远方
tags:

• LeetCode
• 算法
  categories:
• LeetCode破局攻略
  date: 2016-01-01 19:20:00

动态规划系列

• 动态规划详解
• 动态规划答疑篇
• 动态规划设计：最长递增子序列
• 编辑距离
• 经典动态规划问题：高楼扔鸡蛋
• 经典动态规划问题：高楼扔鸡蛋（进阶）
• 动态规划之子序列问题解题模板
• 动态规划之博弈问题
• 贪心算法之区间调度问题
• 动态规划之KMP字符匹配算法
• 团灭 LeetCode 股票买卖问题
• 团灭 LeetCode 打家劫舍问题
• 动态规划之四键键盘
• 动态规划之正则表达
• 最长公共子序列

我们公众号最火的就是动态规划系列的文章，也许是动态规划问题有难度而且有意思，也许因为它是面试常考题型。不管你之前是否害怕动态规划系列的问题，相信这一章的内容足以帮助你消除对动态规划算法的恐惧。
具体来说，动态规划的一般流程就是三步：暴力的递归解法 -> 带备忘录的递归解法 -> 迭代的动态规划解法。
就思考流程来说，就分为一下几步：找到状态和选择 -> 明确 dp 数组/函数的定义 -> 寻找状态之间的关系。
这就是思维模式的框架，本章都会按照以上的模式来解决问题，辅助读者养成这种模式思维，有了方向遇到问题就不会抓瞎，足以解决一般的动态规划问题。

title: 动态规划设计：最长递增子序列
author: 远方
tags:

• LeetCode
• 算法
  categories:
• LeetCode破局攻略
  date: 2016-01-01 19:20:00

动态规划设计：最长递增子序列

很多读者反应，就算看了前文动态规划详解，了解了动态规划的套路，也不会写状态转移方程，没有思路，怎么办？本文就借助「最长递增子序列」来讲一种设计动态规划的通用技巧：数学归纳思想。
最长递增子序列（Longest Increasing Subsequence，简写 LIS）是比较经典的一个问题，比较容易想到的是动态规划解法，时间复杂度 O(N^2)，我们借这个问题来由浅入深讲解如何写动态规划。比较难想到的是利用二分查找，时间复杂度是 O(NlogN)，我们通过一种简单的纸牌游戏来辅助理解这种巧妙的解法。
先看一下题目，很容易理解：

注意「子序列」和「子串」这两个名词的区别，子串一定是连续的，而子序列不一定是连续的。下面先来一步一步设计动态规划算法解决这个问题。

一、动态规划解法

动态规划的核心设计思想是数学归纳法。
相信大家对数学归纳法都不陌生，高中就学过，而且思路很简单。比如我们想证明一个数学结论，那么我们先假设这个结论在 $k<n$ 时成立，然后想办法证明 $k=n$ 的时候此结论也成立。如果能够证明出来，那么就说明这个结论对于 k 等于任何数都成立。
类似的，我们设计动态规划算法，不是需要一个 dp 数组吗？我们可以假设 $dp[0…i-1]$ 都已经被算出来了，然后问自己：怎么通过这些结果算出 dp[i]？
直接拿最长递增子序列这个问题举例你就明白了。不过，首先要定义清楚 dp 数组的含义，即 dp[i] 的值到底代表着什么？
我们的定义是这样的：dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度。
举两个例子：

算法演进的过程是这样的，：

根据这个定义，我们的最终结果（子序列的最大长度）应该是 dp 数组中的最大值。

1
2
3
4
5

int res = 0;
for (int i = 0; i < dp.size(); i++) {
    res = Math.max(res, dp[i]);
}
return res;

读者也许会问，刚才这个过程中每个 dp[i] 的结果是我们肉眼看出来的，我们应该怎么设计算法逻辑来正确计算每个 dp[i] 呢？
这就是动态规划的重头戏了，要思考如何进行状态转移，这里就可以使用数学归纳的思想：
我们已经知道了 $dp[0…4]$ 的所有结果，我们如何通过这些已知结果推出 $dp[5]$ 呢？

根据刚才我们对 dp 数组的定义，现在想求 dp[5] 的值，也就是想求以 nums[5] 为结尾的最长递增子序列。
nums[5] = 3，既然是递增子序列，我们只要找到前面那些结尾比 3 小的子序列，然后把 3 接到最后，就可以形成一个新的递增子序列，而且这个新的子序列长度加一。
当然，可能形成很多种新的子序列，但是我们只要最长的，把最长子序列的长度作为 dp[5] 的值即可。

1
2
3
4

for (int j = 0; j < i; j++) {
    if (nums[i] > nums[j]) 
        dp[i] = Math.max(dp[i], dp[j] + 1);
}

这段代码的逻辑就可以算出 dp[5]。到这里，这道算法题我们就基本做完了。读者也许会问，我们刚才只是算了 dp[5] 呀，dp[4], dp[3] 这些怎么算呢？
类似数学归纳法，你已经可以算出 dp[5] 了，其他的就都可以算出来：

1
2
3
4
5
6

for (int i = 0; i < nums.length; i++) {
    for (int j = 0; j < i; j++) {
        if (nums[i] > nums[j]) 
            dp[i] = Math.max(dp[i], dp[j] + 1);
    }
}

还有一个细节问题，dp 数组应该全部初始化为 1，因为子序列最少也要包含自己，所以长度最小为 1。下面我们看一下完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

public int lengthOfLIS(int[] nums) {
    int[] dp = new int[nums.length];
    // dp 数组全都初始化为 1
    Arrays.fill(dp, 1);
    for (int i = 0; i < nums.length; i++) {
        for (int j = 0; j < i; j++) {
            if (nums[i] > nums[j]) 
                dp[i] = Math.max(dp[i], dp[j] + 1);
        }
    }
    
    int res = 0;
    for (int i = 0; i < dp.length; i++) {
        res = Math.max(res, dp[i]);
    }
    return res;
}

至此，这道题就解决了，时间复杂度 O(N^2)。总结一下动态规划的设计流程：
首先明确 dp 数组所存数据的含义。这步很重要，如果不得当或者不够清晰，会阻碍之后的步骤。
然后根据 dp 数组的定义，运用数学归纳法的思想，假设 $dp[0…i-1]$ 都已知，想办法求出 $dp[i]$，一旦这一步完成，整个题目基本就解决了。
但如果无法完成这一步，很可能就是 dp 数组的定义不够恰当，需要重新定义 dp 数组的含义；或者可能是 dp 数组存储的信息还不够，不足以推出下一步的答案，需要把 dp 数组扩大成二维数组甚至三维数组。
最后想一想问题的 base case 是什么，以此来初始化 dp 数组，以保证算法正确运行。

二、二分查找解法

这个解法的时间复杂度会将为 O(NlogN)，但是说实话，正常人基本想不到这种解法（也许玩过某些纸牌游戏的人可以想出来）。所以如果大家了解一下就好，正常情况下能够给出动态规划解法就已经很不错了。
根据题目的意思，我都很难想象这个问题竟然能和二分查找扯上关系。其实最长递增子序列和一种叫做 patience game 的纸牌游戏有关，甚至有一种排序方法就叫做 patience sorting（耐心排序）。
为了简单期间，后文跳过所有数学证明，通过一个简化的例子来理解一下思路。
首先，给你一排扑克牌，我们像遍历数组那样从左到右一张一张处理这些扑克牌，最终要把这些牌分成若干堆。

处理这些扑克牌要遵循以下规则：
只能把点数小的牌压到点数比它大的牌上。如果当前牌点数较大没有可以放置的堆，则新建一个堆，把这张牌放进去。如果当前牌有多个堆可供选择，则选择最左边的堆放置。
比如说上述的扑克牌最终会被分成这样 5 堆（我们认为 A 的值是最大的，而不是 1）。

为什么遇到多个可选择堆的时候要放到最左边的堆上呢？因为这样可以保证牌堆顶的牌有序（2, 4, 7, 8, Q），证明略。

按照上述规则执行，可以算出最长递增子序列，牌的堆数就是最长递增子序列的长度，证明略。

我们只要把处理扑克牌的过程编程写出来即可。每次处理一张扑克牌不是要找一个合适的牌堆顶来放吗，牌堆顶的牌不是有序吗，这就能用到二分查找了：用二分查找来搜索当前牌应放置的位置。
PS：旧文二分查找算法详解详细介绍了二分查找的细节及变体，这里就完美应用上了。如果没读过强烈建议阅读。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

public int lengthOfLIS(int[] nums) {
    int[] top = new int[nums.length];
    // 牌堆数初始化为 0
    int piles = 0;
    for (int i = 0; i < nums.length; i++) {
        // 要处理的扑克牌
        int poker = nums[i];
        /***** 搜索左侧边界的二分查找 *****/
        int left = 0, right = piles;
        while (left < right) {
            int mid = (left + right) / 2;
            if (top[mid] > poker) {
                right = mid;
            } else if (top[mid] < poker) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        /*********************************/
        
        // 没找到合适的牌堆，新建一堆
        if (left == piles) piles++;
        // 把这张牌放到牌堆顶
        top[left] = poker;
    }
    // 牌堆数就是 LIS 长度
    return piles;
}

至此，二分查找的解法也讲解完毕。
这个解法确实很难想到。首先涉及数学证明，谁能想到按照这些规则执行，就能得到最长递增子序列呢？其次还有二分查找的运用，要是对二分查找的细节不清楚，给了思路也很难写对。
所以，这个方法作为思维拓展好了。但动态规划的设计方法应该完全理解：假设之前的答案已知，利用数学归纳的思想正确进行状态的推演转移，最终得到答案。

上一篇：动态规划答疑篇
下一篇：编辑距离
目录

title: 子序列问题模板
author: 远方
tags:

• LeetCode
• 算法
  categories:
• LeetCode破局攻略
  date: 2016-01-01 19:20:00

动态规划之子序列问题解题模板

子序列问题是常见的算法问题，而且并不好解决。
首先，子序列问题本身就相对子串、子数组更困难一些，因为前者是不连续的序列，而后两者是连续的，就算穷举你都不一定会，更别说求解相关的算法问题了。
而且，子序列问题很可能涉及到两个字符串，比如前文「最长公共子序列」，如果没有一定的处理经验，真的不容易想出来。所以本文就来扒一扒子序列问题的套路，其实就有两种模板，相关问题只要往这两种思路上想，十拿九稳。
一般来说，这类问题都是让你求一个最长子序列，因为最短子序列就是一个字符嘛，没啥可问的。一旦涉及到子序列和最值，那几乎可以肯定，**考察的是动态规划技巧，时间复杂度一般都是 O(n^2)**。
原因很简单，你想想一个字符串，它的子序列有多少种可能？起码是指数级的吧，这种情况下，不用动态规划技巧，还想怎么着？
既然要用动态规划，那就要定义 dp 数组，找状态转移关系。我们说的两种思路模板，就是 dp 数组的定义思路。不同的问题可能需要不同的 dp 数组定义来解决。

一、两种思路

1、第一种思路模板是一个一维的 dp 数组：

1
2
3
4
5
6
7

int n = array.length;
int[] dp = new int[n];
for (int i = 1; i < n; i++) {
    for (int j = 0; j < i; j++) {
        dp[i] = 最值(dp[i], dp[j] + ...)
    }
}

举个我们写过的例子「最长递增子序列」，在这个思路中 dp 数组的定义是：
在子数组 array[0..i] 中，我们要求的子序列（最长递增子序列）的长度是 dp[i]**。
为啥最长递增子序列需要这种思路呢？前文说得很清楚了，因为这样符合归纳法，可以找到状态转移的关系，这里就不具体展开了。
**2、第二种思路模板是一个二维的 dp 数组：

1
2
3
4
5
6
7
8
9
10

int n = arr.length;
int[][] dp = new dp[n][n];
for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
        if (arr[i] == arr[j]) 
            dp[i][j] = dp[i][j] + ...
        else
            dp[i][j] = 最值(...)
    }
}

这种思路运用相对更多一些，尤其是涉及两个字符串/数组的子序列，比如前文讲的「最长公共子序列」。本思路中 dp 数组含义又分为「只涉及一个字符串」和「涉及两个字符串」两种情况。
2.1 涉及两个字符串/数组时（比如最长公共子序列），dp 数组的含义如下：
在子数组 arr1[0..i] 和子数组 arr2[0..j] 中，我们要求的子序列（最长公共子序列）长度为 dp[i][j]**。
**2.2 只涉及一个字符串/数组时（比如本文要讲的最长回文子序列），dp 数组的含义如下：
**在子数组 array[i..j] 中，我们要求的子序列（最长回文子序列）的长度为 dp[i][j]**。
第一种情况可以参考这两篇旧文：「编辑距离」「公共子序列」
下面就借最长回文子序列这个问题，详解一下第二种情况下如何使用动态规划。

二、最长回文子序列

之前解决了「最长回文子串」的问题，这次提升难度，求最长回文子序列的长度：

我们说这个问题对 dp 数组的定义是：在子串 s[i..j] 中，最长回文子序列的长度为 dp[i][j]**。一定要记住这个定义才能理解算法。
为啥这个问题要这样定义二维的 dp 数组呢？我们前文多次提到，找状态转移需要归纳思维，说白了就是如何从已知的结果推出未知的部分，这样定义容易归纳，容易发现状态转移关系。
具体来说，如果我们想求 dp[i][j]，假设你知道了子问题 dp[i+1][j-1] 的结果（s[i+1..j-1] 中最长回文子序列的长度），你是否能想办法算出 dp[i][j] 的值（s[i..j] 中，最长回文子序列的长度）呢？

可以！这取决于 s[i] 和 s[j] 的字符：
**如果它俩相等，那么它俩加上 s[i+1..j-1] 中的最长回文子序列就是 s[i..j] 的最长回文子序列：

如果它俩不相等，说明它俩不可能同时出现在 s[i..j] 的最长回文子序列中，那么把它俩分别加入 s[i+1..j-1] 中，看看哪个子串产生的回文子序列更长即可：

以上两种情况写成代码就是这样：

1
2
3
4
5
6

if (s[i] == s[j])
    // 它俩一定在最长回文子序列中
    dp[i][j] = dp[i + 1][j - 1] + 2;
else
    // s[i+1..j] 和 s[i..j-1] 谁的回文子序列更长？
    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);

至此，状态转移方程就写出来了，根据 dp 数组的定义，我们要求的就是 dp[0][n - 1]，也就是整个 s 的最长回文子序列的长度。

三、代码实现

首先明确一下 base case，如果只有一个字符，显然最长回文子序列长度是 1，也就是 dp[i][j] = 1 (i == j)。
因为 i 肯定小于等于 j，所以对于那些 i > j 的位置，根本不存在什么子序列，应该初始化为 0。
另外，看看刚才写的状态转移方程，想求 dp[i][j] 需要知道 dp[i+1][j-1]，dp[i+1][j]，dp[i][j-1] 这三个位置；再看看我们确定的 base case，填入 dp 数组之后是这样：

为了保证每次计算 dp[i][j]，左下右方向的位置已经被计算出来，只能斜着遍历或者反着遍历：

我选择反着遍历，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

int longestPalindromeSubseq(string s) {
    int n = s.size();
    // dp 数组全部初始化为 0
    vector<vector<int>> dp(n, vector<int>(n, 0));
    // base case
    for (int i = 0; i < n; i++)
        dp[i][i] = 1;
    // 反着遍历保证正确的状态转移
    for (int i = n - 1; i >= 0; i--) {
        for (int j = i + 1; j < n; j++) {
            // 状态转移方程
            if (s[i] == s[j])
                dp[i][j] = dp[i + 1][j - 1] + 2;
            else
                dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
        }
    }
    // 整个 s 的最长回文子串长度
    return dp[0][n - 1];
}

至此，最长回文子序列的问题就解决了。

上一篇：经典动态规划问题：高楼扔鸡蛋（进阶）
下一篇：动态规划之博弈问题
目录