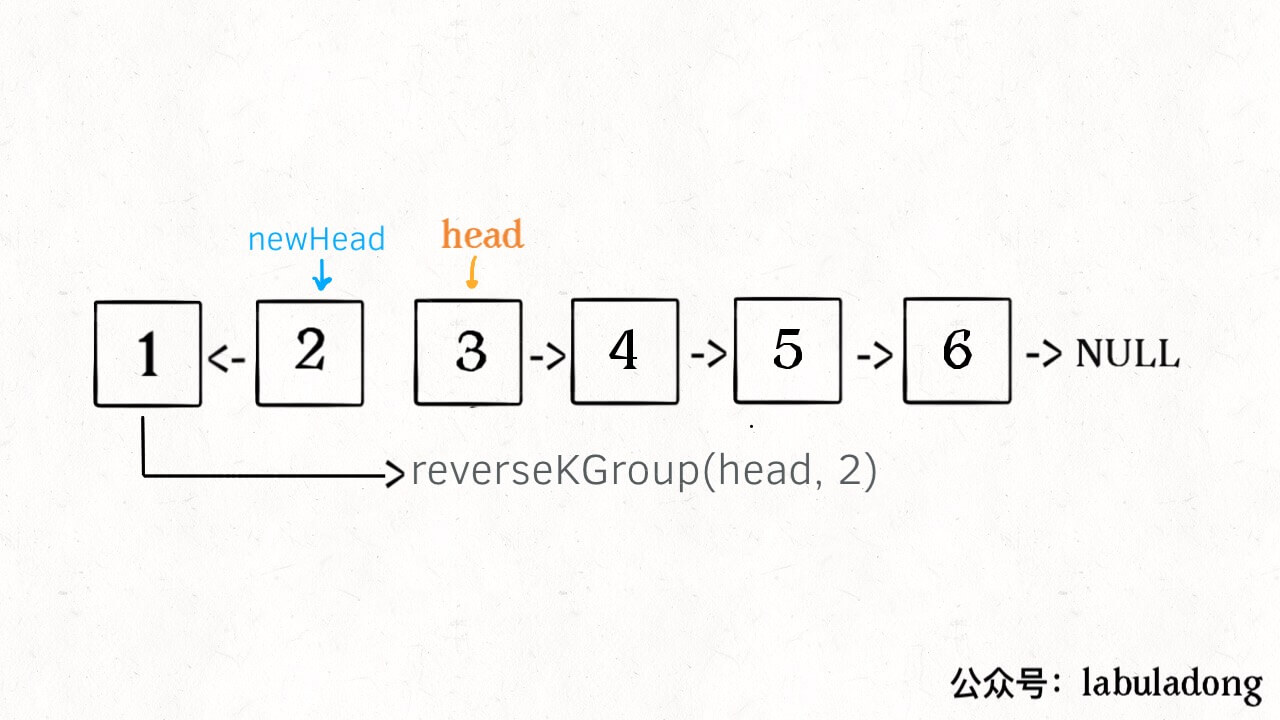
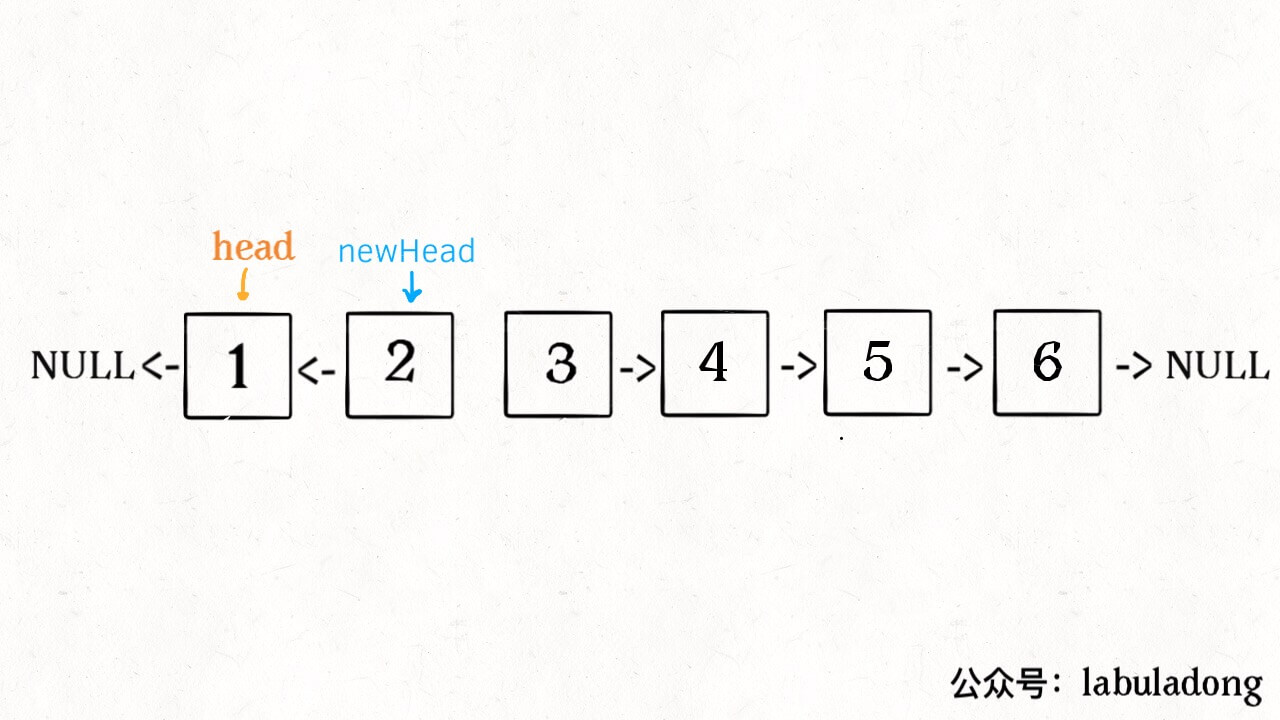
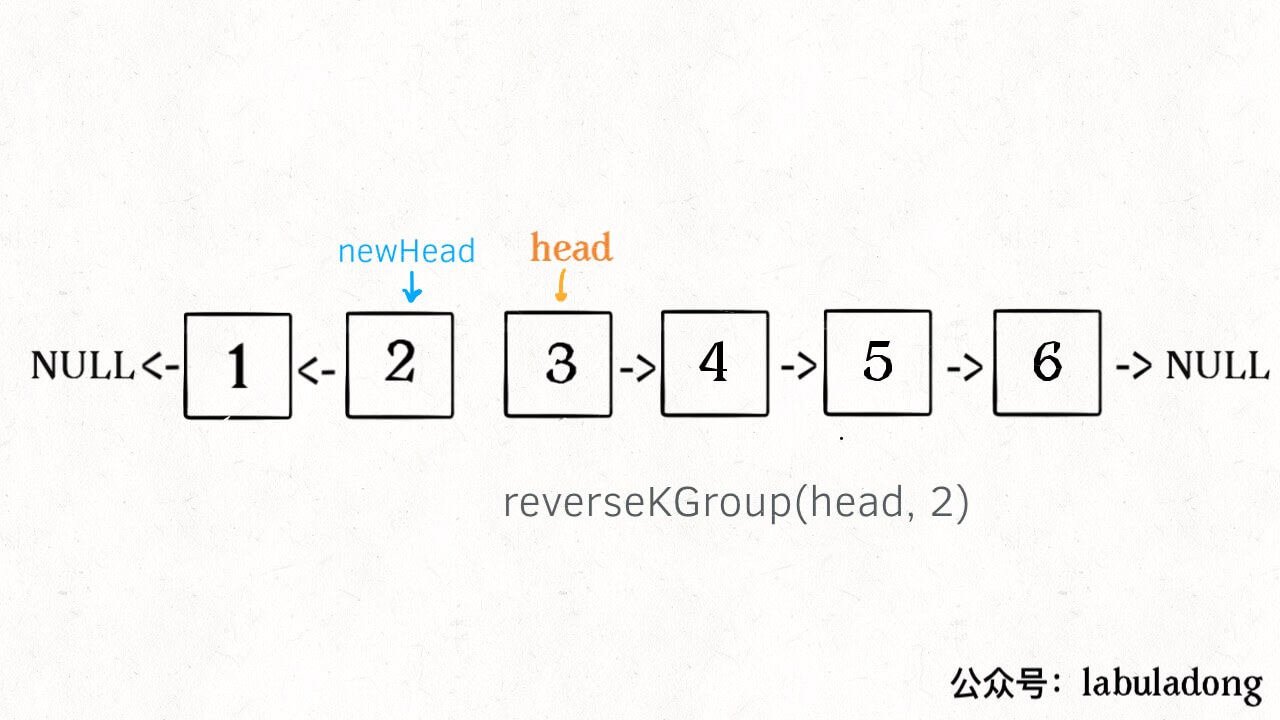
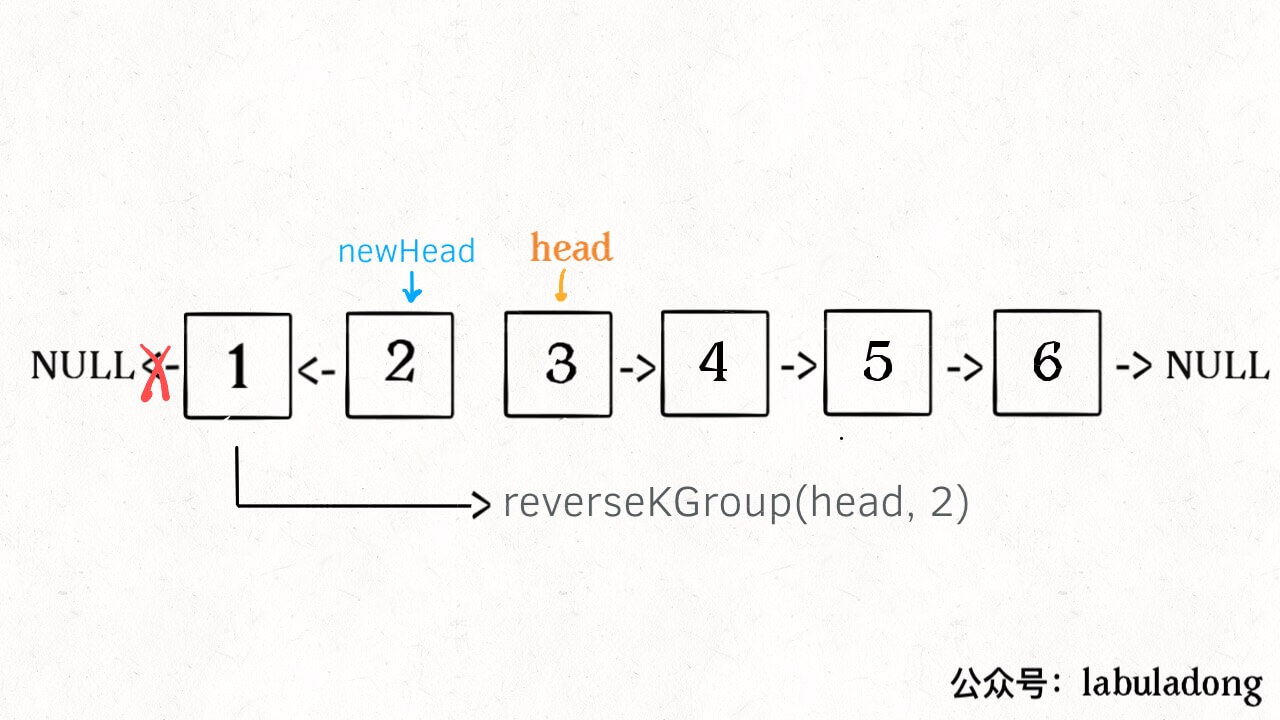
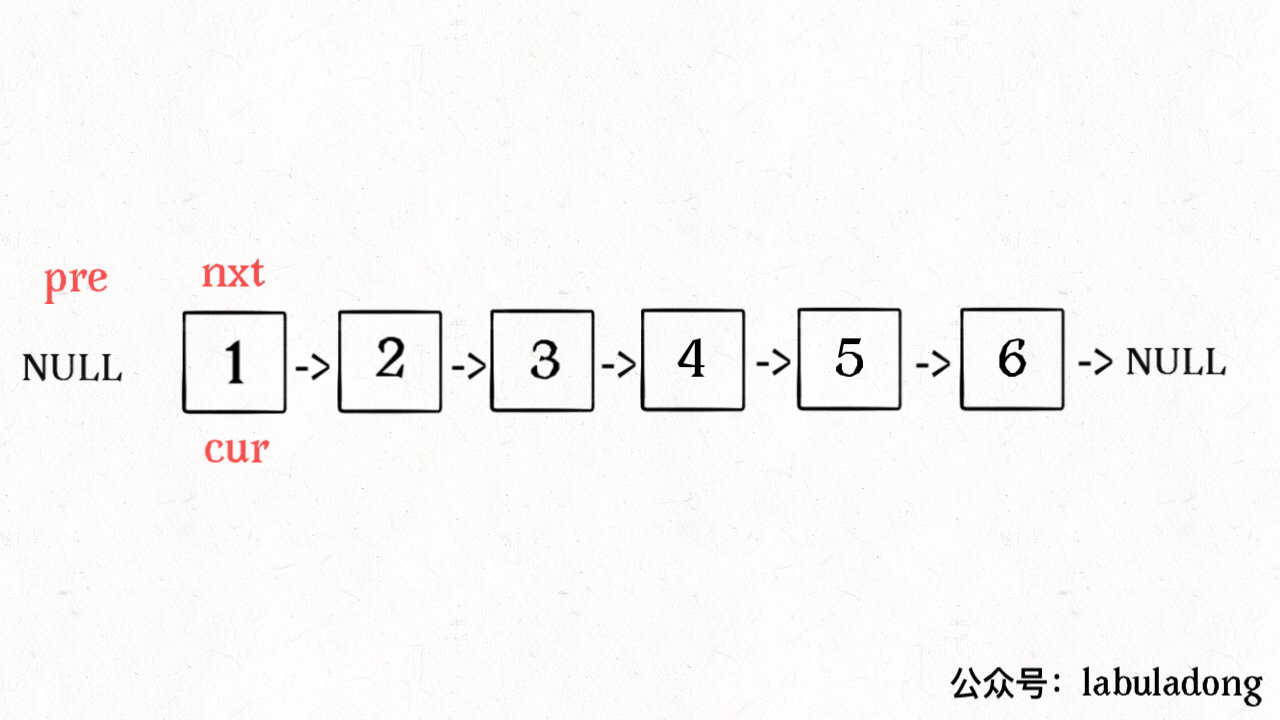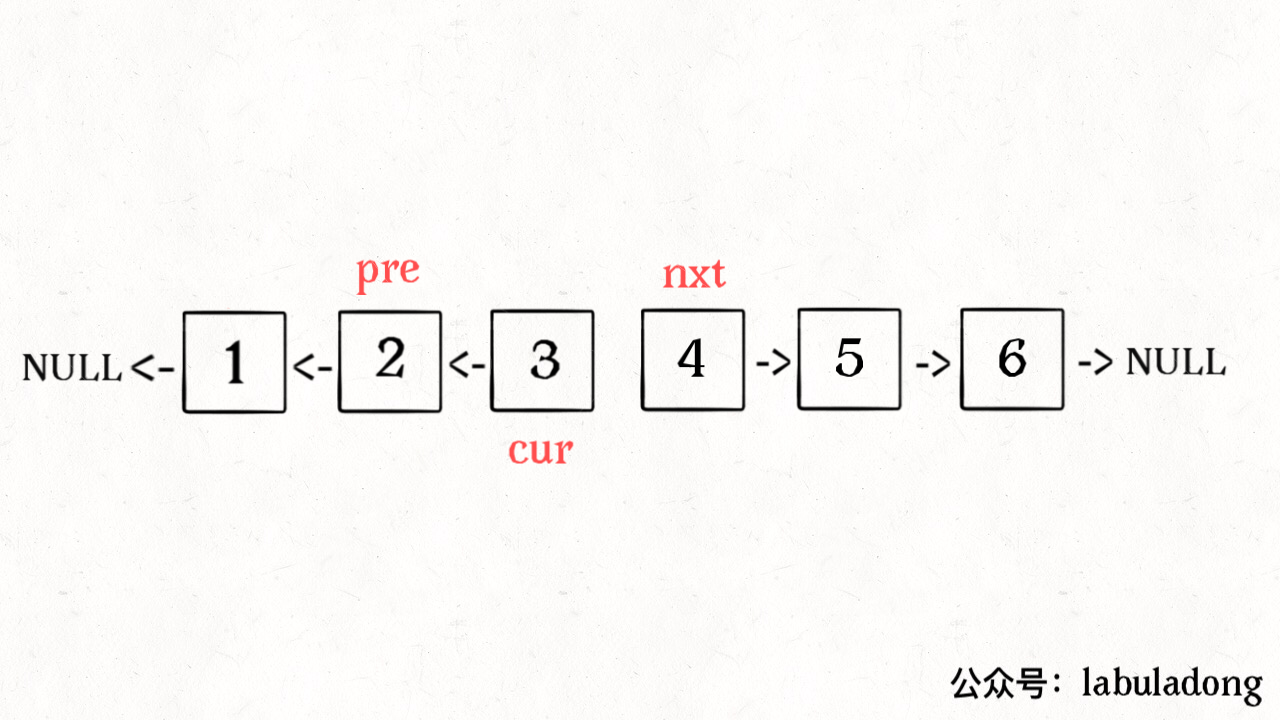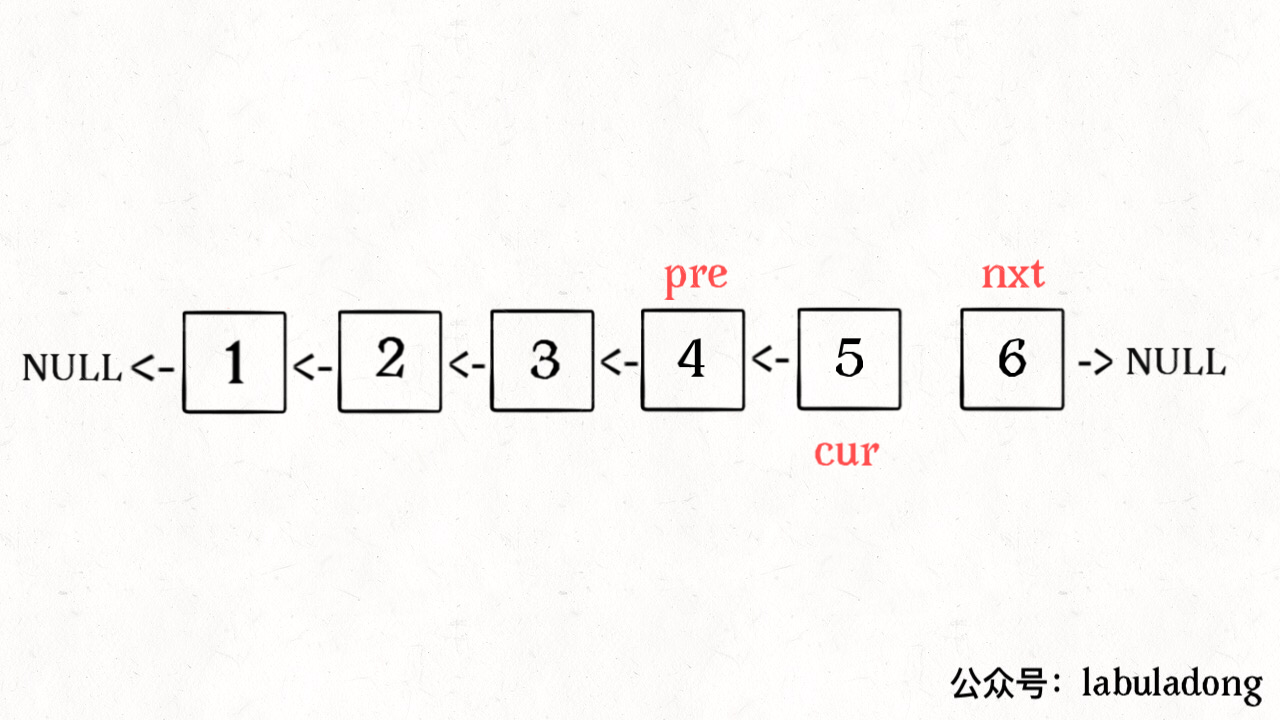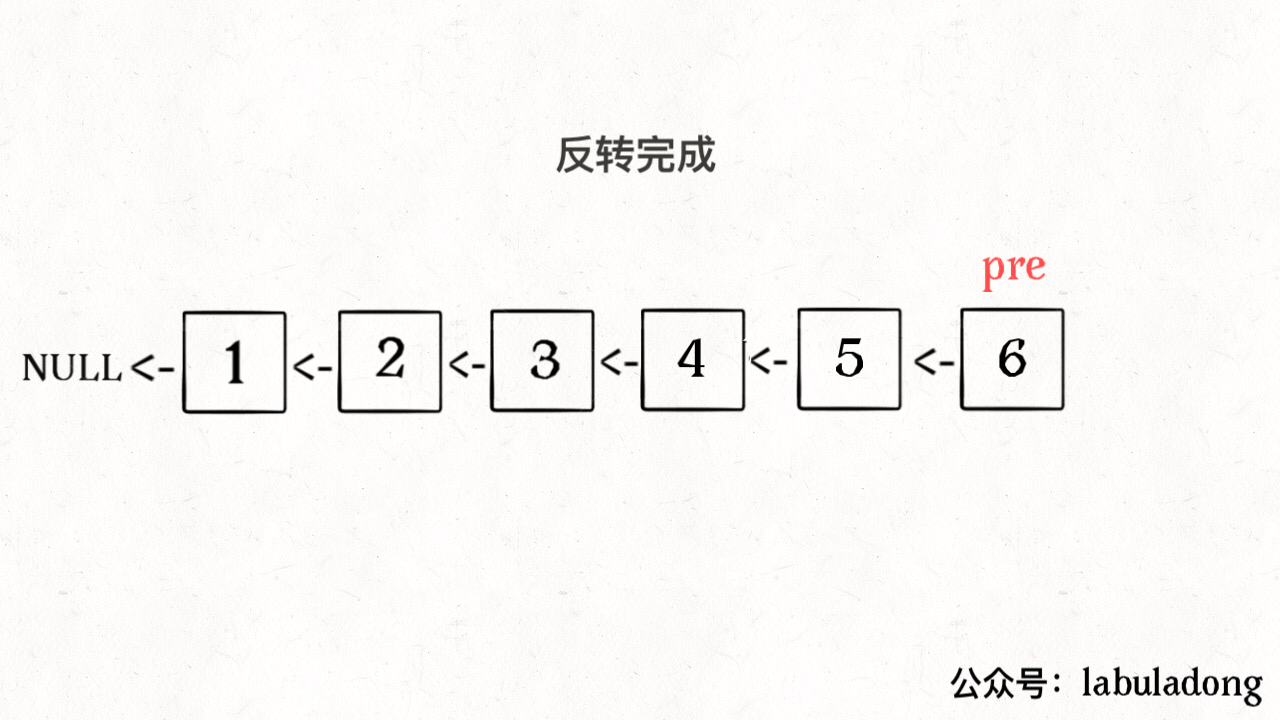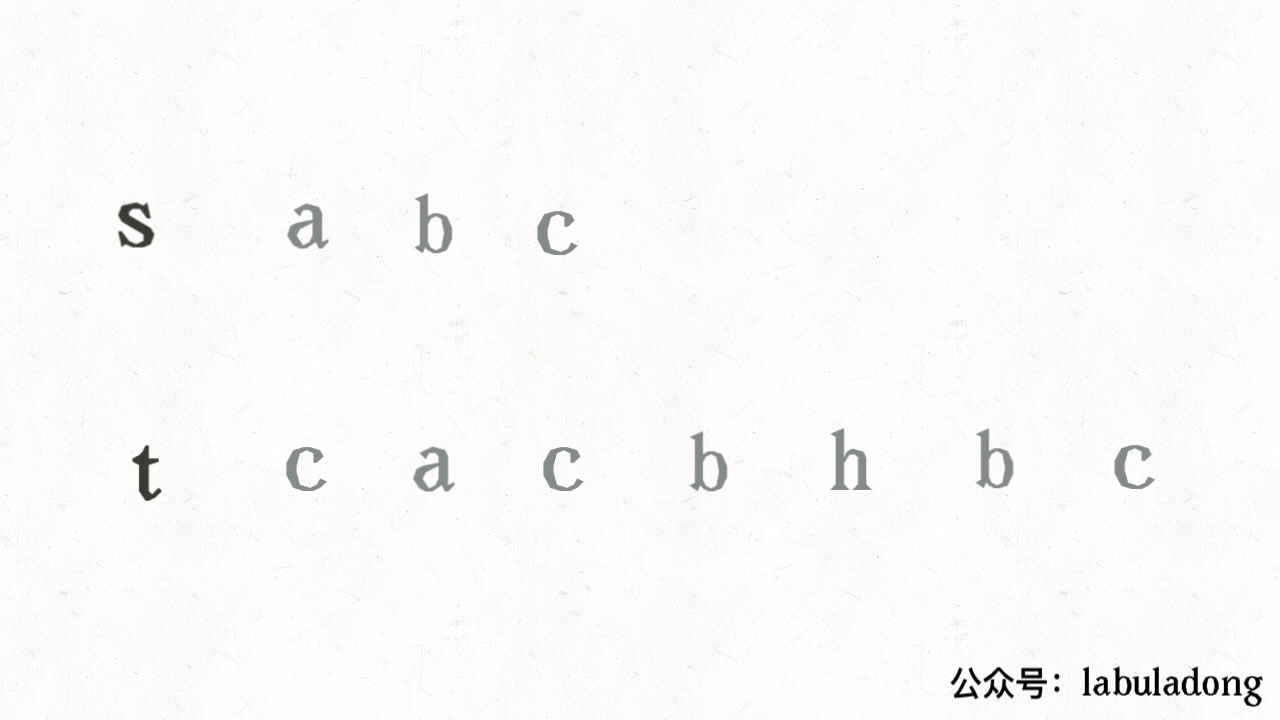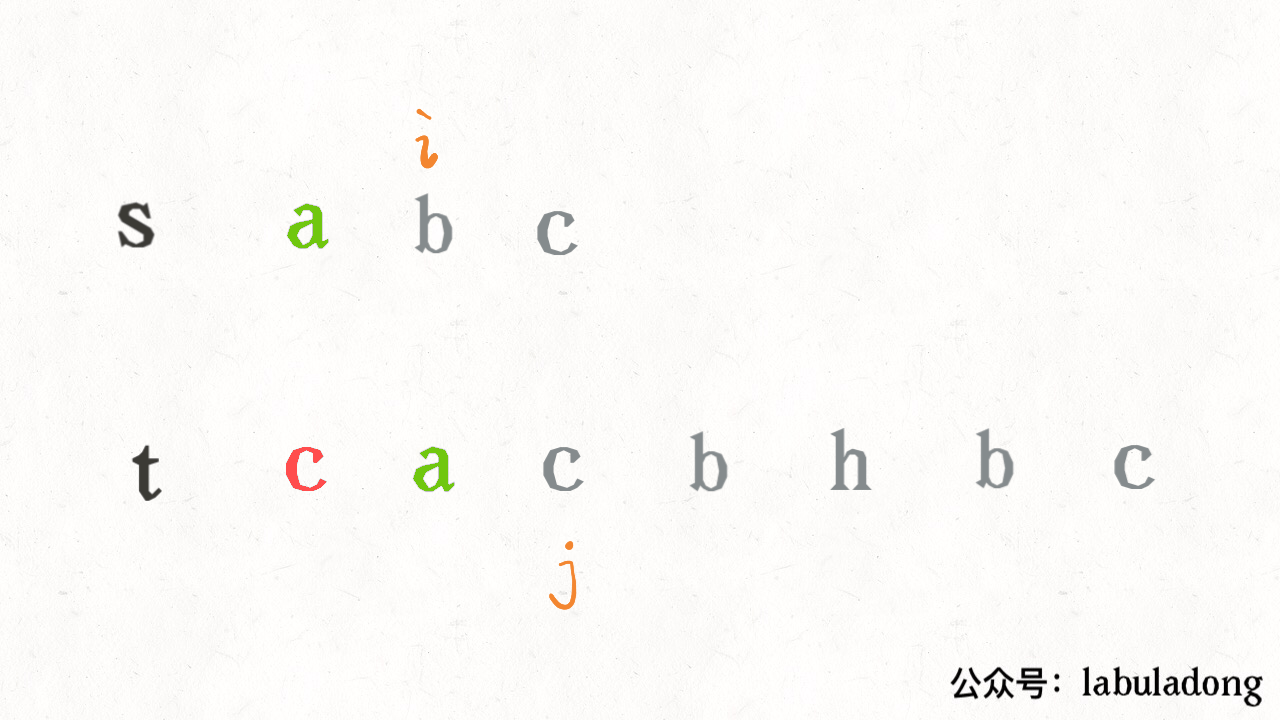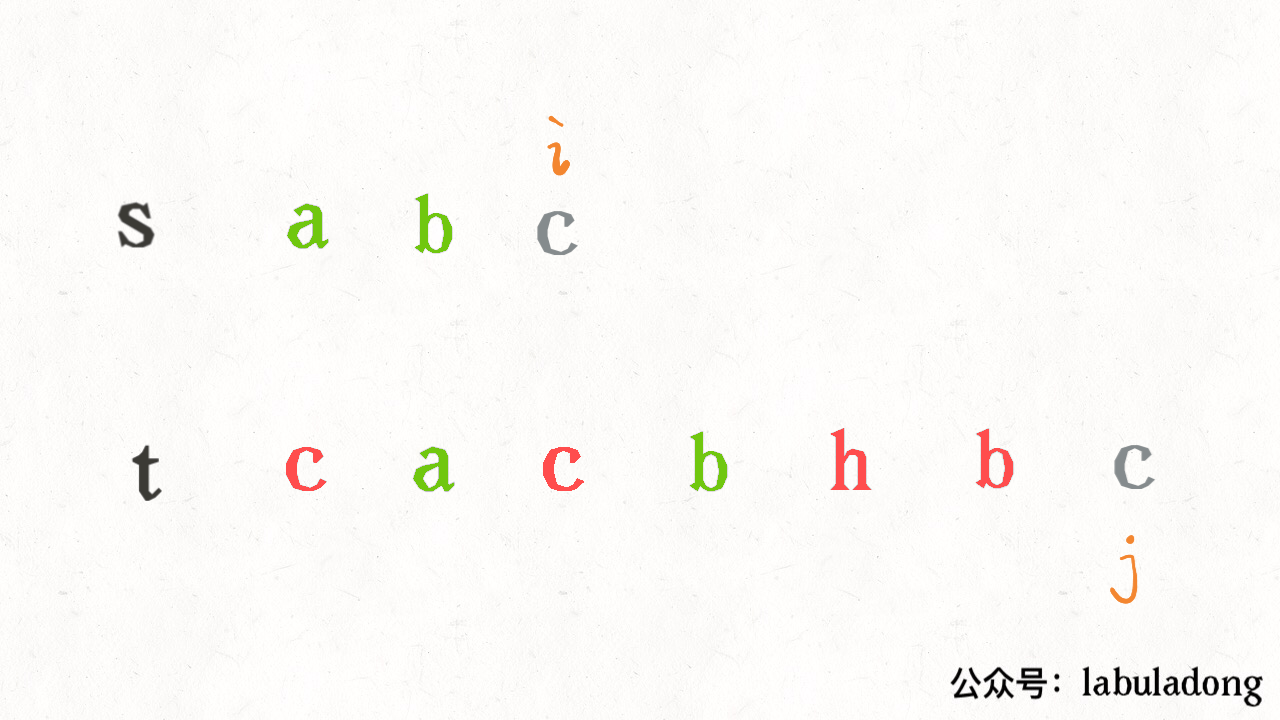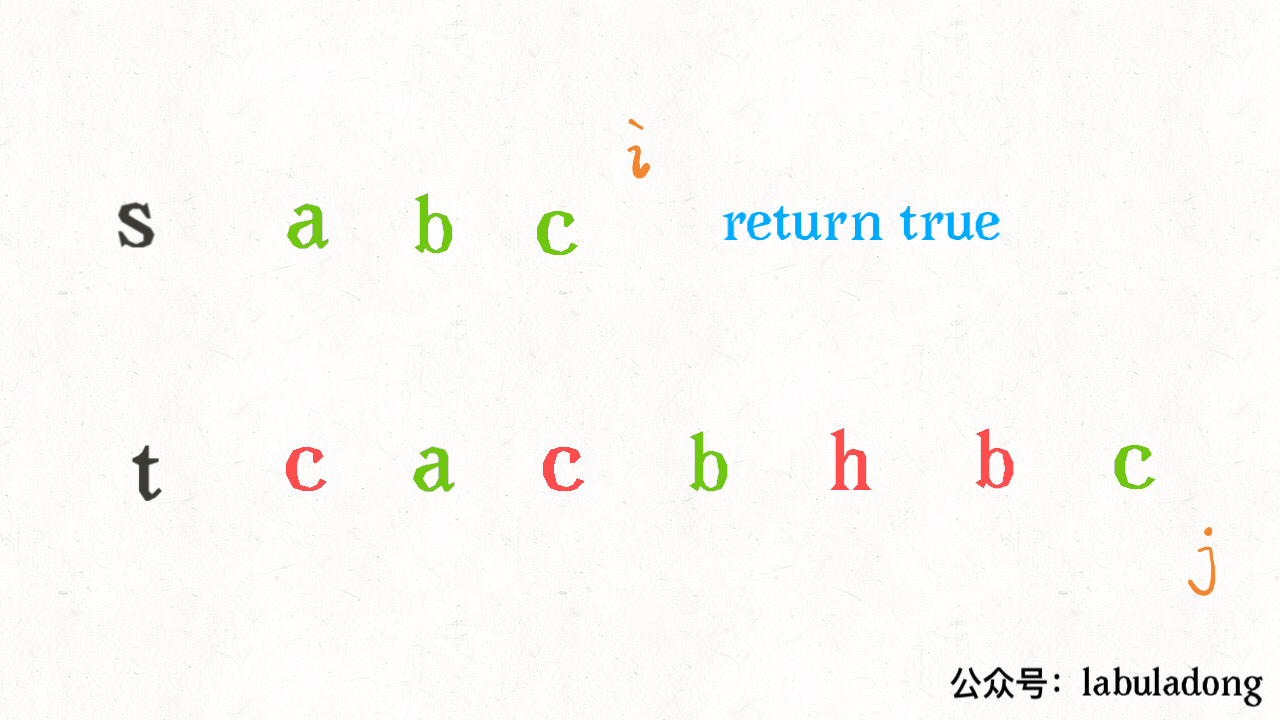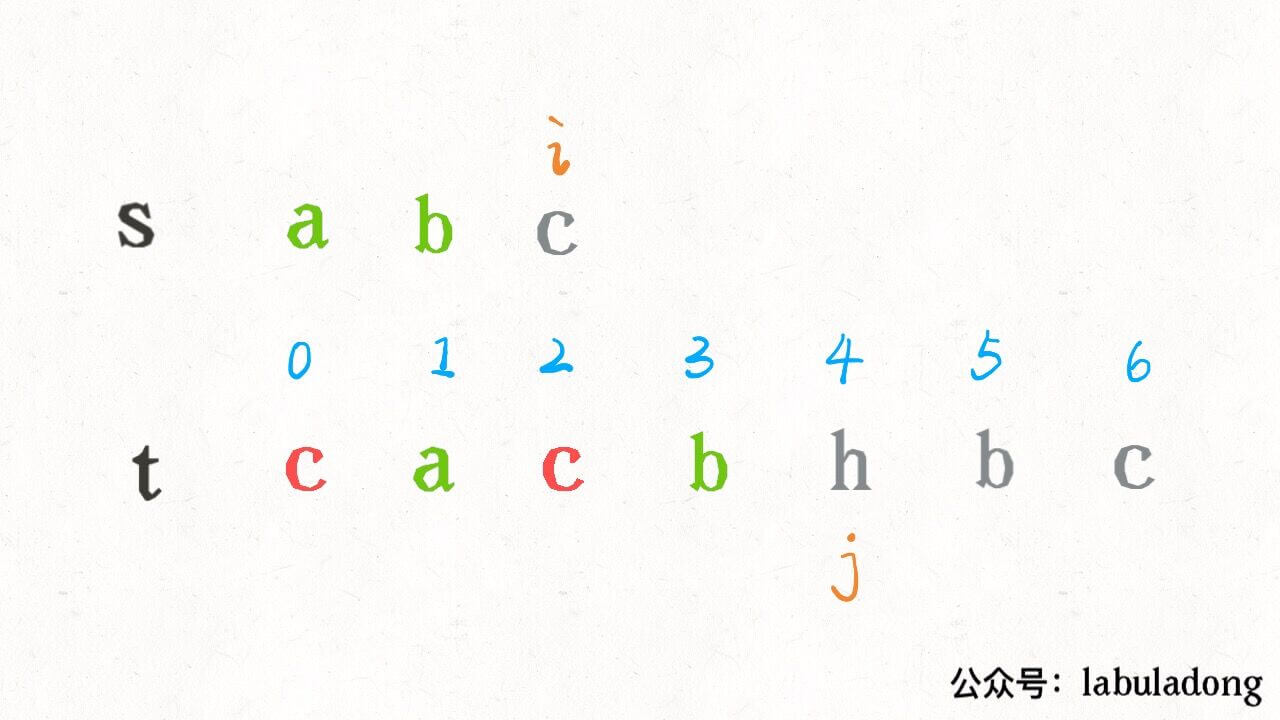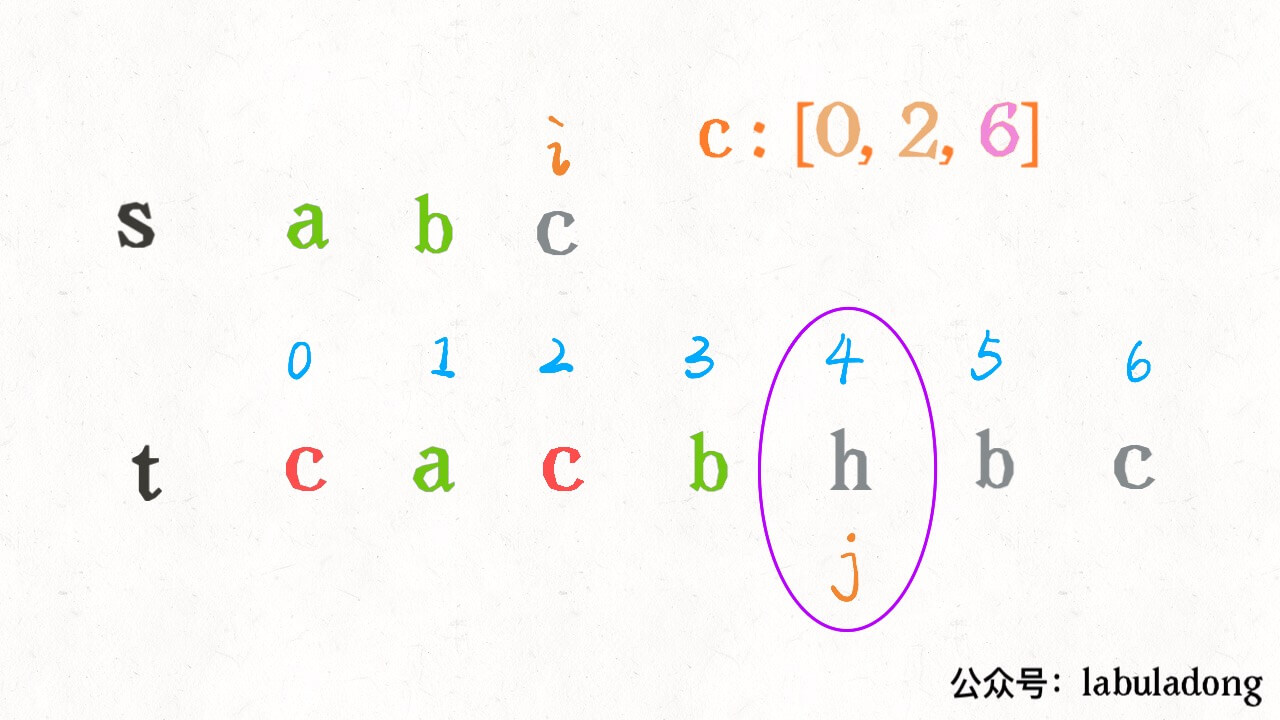算法学习之路
之前发的那篇关于框架性思维的文章,我也发到了不少其他圈子,受到了大家的普遍好评,这一点我真的没想到,首先感谢大家的认可,我会更加努力,写出通俗易懂的算法文章。
有很多朋友问我数据结构和算法到底该怎么学,尤其是很多朋友说自己是「小白」,感觉这些东西好难啊,就算看了之前的「框架思维」,也感觉自己刷题乏力,希望我能聊聊我从一个非科班小白一路是怎么学过来的。
首先要给怀有这样疑问的朋友鼓掌,因为你现在已经「知道自己不知道」,而且开始尝试学习、刷题、寻求帮助,能做到这一点本身就是及其困难的。
关于「框架性思维」,对于一个小白来说,可能暂时无法完全理解(如果你能理解,说明你水平已经不错啦,不是小白啦)。就像软件工程,对于我这种没带过项目的人来说,感觉其内容枯燥乏味,全是废话,但是对于一个带过团队的人,他就会觉得软件工程里的每一句话都是精华。暂时不太理解没关系,留个印象,功夫到了很快就明白了。
下面写一写我一路过来的一些经验。如果你已经看过很多「如何高效刷题」「如何学习算法」的文章,却还是没有开始行动并坚持下去,本文的第五点就是写给你的。
我觉得之所以有时候认为自己是「小白」,是由于知识某些方面的空白造成的。具体到数据结构的学习,无非就是两个问题搞得不太清楚:这是啥?有啥用?
举个例子,比如说你看到了「栈」这个名词,老师可能会讲这些关键词:先进后出、函数堆栈等等。但是,对于初学者,这些描述属于文学词汇,没有实际价值,没有解决最基本的两个问题。如何回答这两个基本问题呢?回答「这是啥」需要看教科书,回答「有啥用」需要刷算法题。
一、这是啥?
这个问题最容易解决,就像一层窗户纸,你只要随便找本书看两天,自己动手实现一个「队列」「栈」之类的数据结构,就能捅破这层窗户纸。
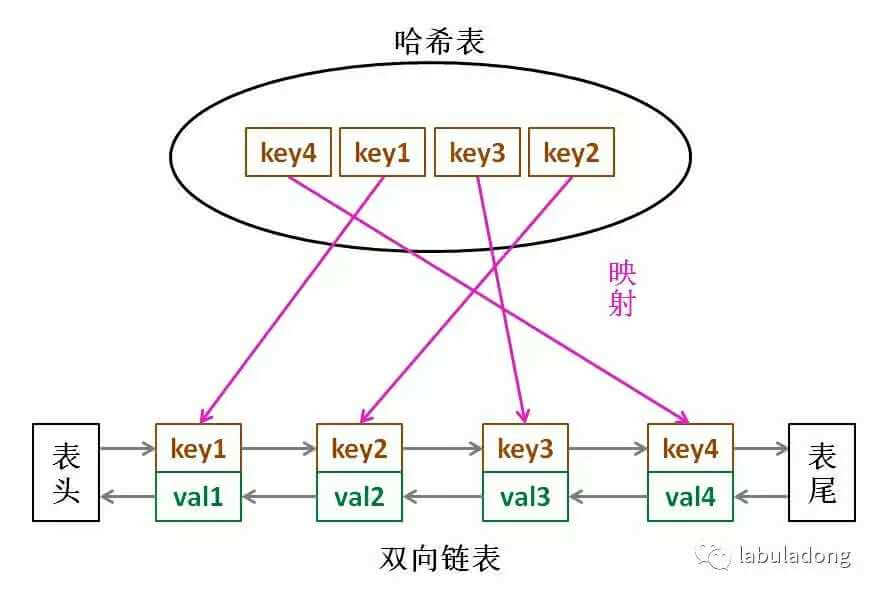
这时候你就能理解「框架思维」文章中的前半部分了:数据结构无非就是数组、链表为骨架的一些特定操作而已;每个数据结构实现的功能无非增删查改罢了。
比如说「列队」这个数据结构,无非就是基于数组或者链表,实现 enqueue 和 dequeue 两个方法。这两个方法就是增和删呀,连查和改的方法都不需要。
二、有啥用?
解决这个问题,就涉及算法的设计了,是个持久战,需要经常进行抽象思考,刷算法题,培养「计算机思维」。
之前的文章讲了,算法就是对数据结构准确而巧妙的运用。常用算法问题也就那几大类,算法题无非就是不断变换场景,给那几个算法框架套上不同的皮。刷题,就是在锻炼你的眼力,看你能不能看穿问题表象揪出相应的解法框架。
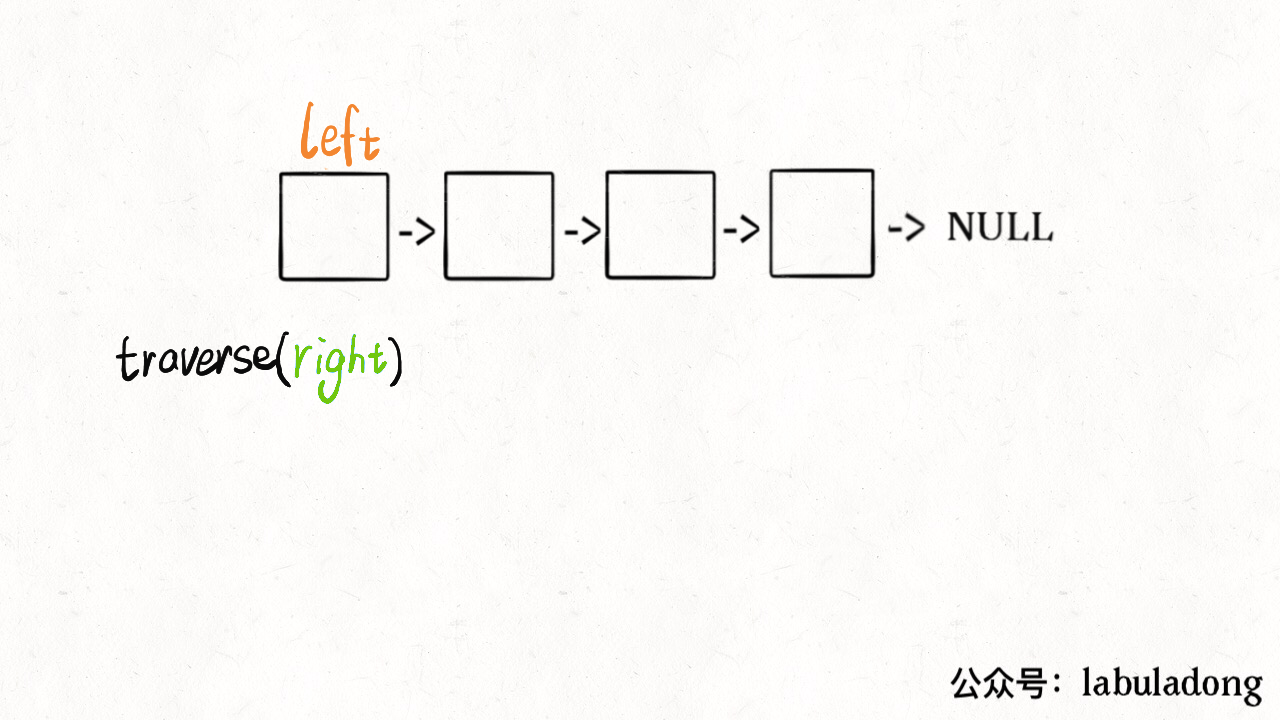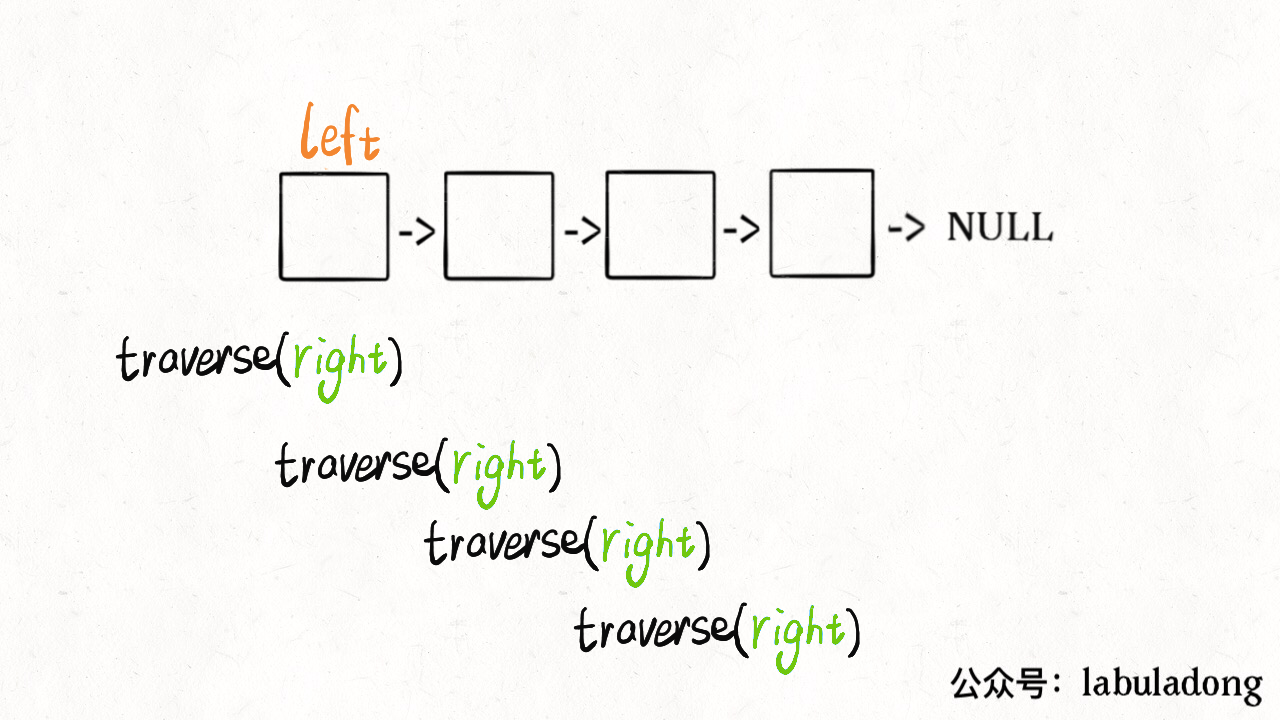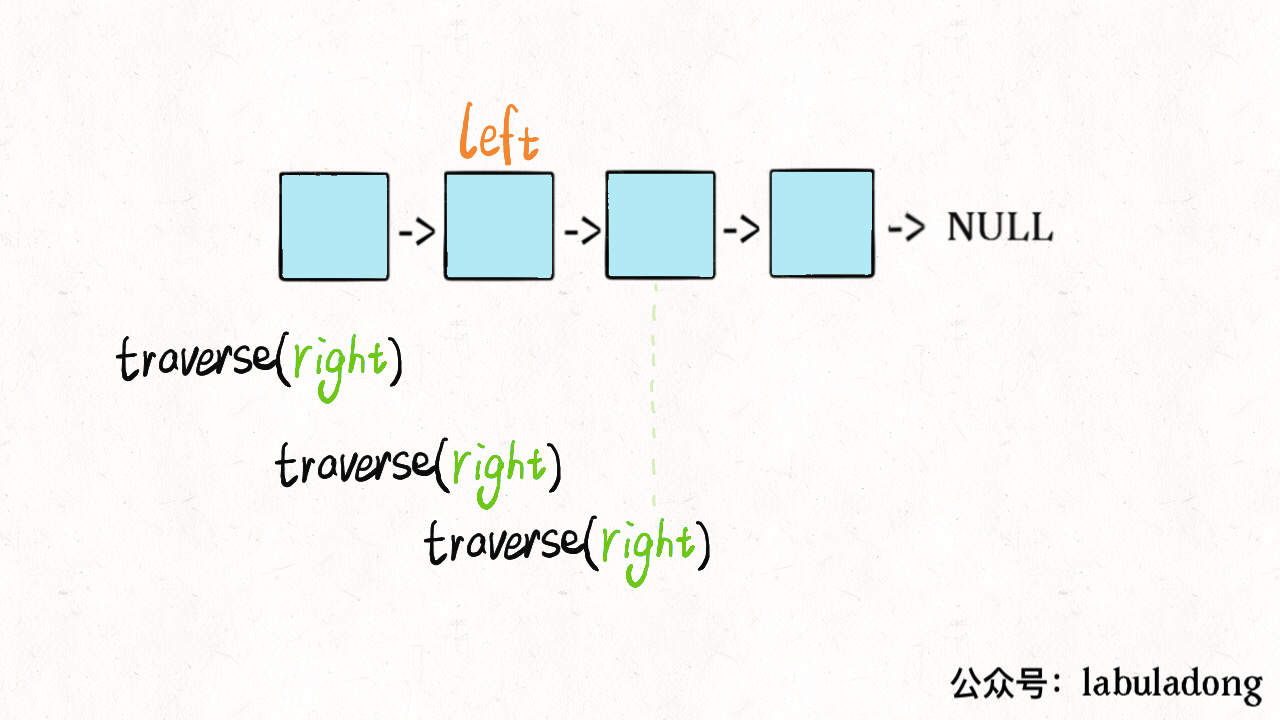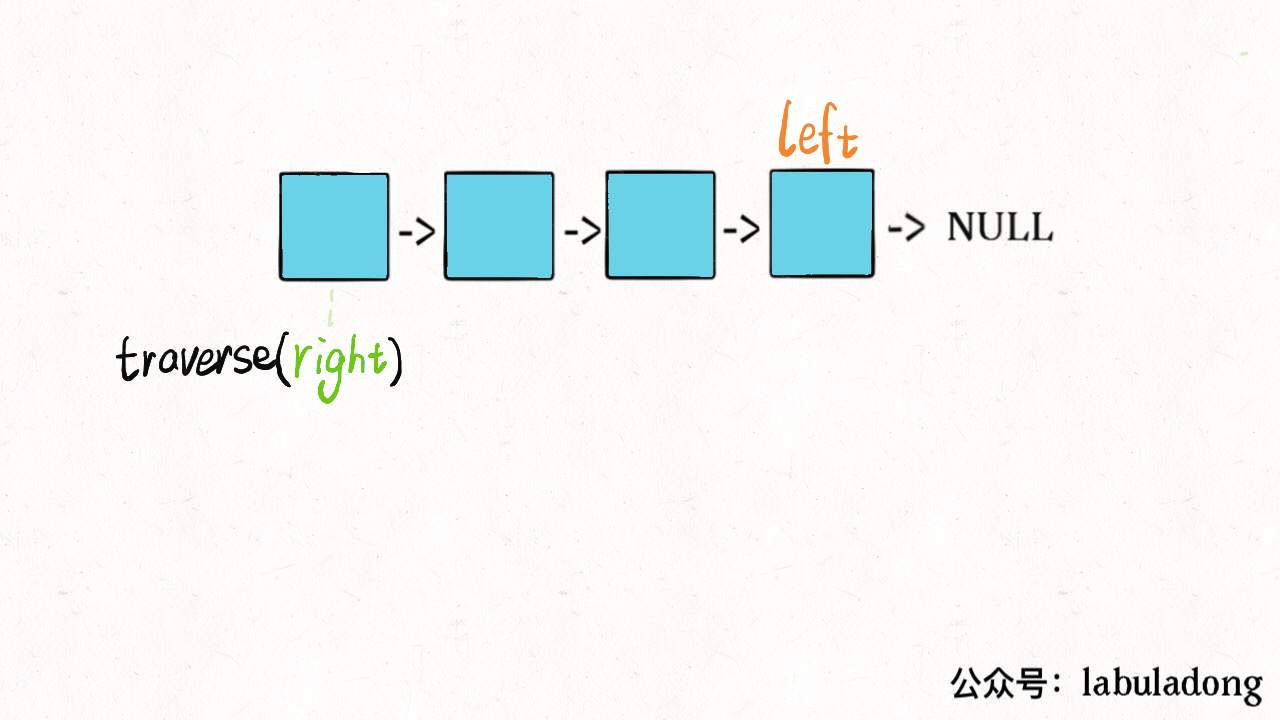
比如说,让你求解一个迷宫,你要把这个问题层层抽象:迷宫 -> 图的遍历 -> N 叉树的遍历 -> 二叉树的遍历。然后让框架指导你写具体的解法。
抽象问题,直击本质,是刷题中你需要刻意培养的能力。
三、如何看书
直接推荐一本公认的好书,《算法第 4 版》,我一般简写成《算法4》。不要蜻蜓点水,这本书你能选择性的看上 50%,基本上就达到平均水平了。别怕这本书厚,因为起码有三分之一不用看,下面讲讲怎么看这本书。
看书仍然遵循递归的思想:自顶向下,逐步求精。
这本书知识结构合理,讲解也清楚,所以可以按顺序学习。书中正文的算法代码一定要亲自敲一遍,因为这些真的是扎实的基础,要认真理解。不要以为自己看一遍就看懂了,不动手的话理解不了的。但是,开头部分的基础可以酌情跳过;书中的数学证明,如不影响对算法本身的理解,完全可以跳过;章节最后的练习题,也可以全部跳过。这样一来,这本书就薄了很多。
相信读者现在已经认可了「框架性思维」的重要性,这种看书方式也是一种框架性策略,抓大放小,着重理解整体的知识架构,而忽略证明、练习题这种细节问题,即保持自己对新知识的好奇心,避免陷入无限的细节被劝退。
当然,《算法4》到后面的内容也比较难了,比如那几个著名的串算法,以及正则表达式算法。这些属于「经典算法」,看个人接受能力吧,单说刷 LeetCode 的话,基本用不上,量力而行即可。
四、如何刷题
首先声明一下,算法和数学水平没关系,和编程语言也没关系,你爱用什么语言用什么。算法,主要是培养一种新的思维方式。所谓「计算机思维」,就跟你考驾照一样,你以前骑自行车,有一套自行车的规则和技巧,现在你开汽车,就需要适应并练习开汽车的规则和技巧。
LeetCode 上的算法题和前面说的「经典算法」不一样,我们权且称为「解闷算法」吧,因为很多题目都比较有趣,有种在做奥数题或者脑筋急转弯的感觉。比如说,让你用队列实现一个栈,或者用栈实现一个队列,以及不用加号做加法,开脑洞吧?
当然,这些问题虽然看起来无厘头,实际生活中也用不到,但是想解决这些问题依然要靠数据结构以及对基础知识的理解,也许这就是很多公司面试都喜欢出这种「智力题」的原因。下面说几点技巧吧。
尽量刷英文版的 LeetCode,中文版的“力扣”是阉割版,不仅很多题目没有答案,而且连个讨论区都没有。英文版的是真的很良心了,很多问题都有官方解答,详细易懂。而且讨论区(Discuss)也沉淀了大量优质内容,甚至好过官方解答。真正能打开你思路的,很可能是讨论区各路大神的思路荟萃。
PS:如果有的英文题目实在看不懂,有个小技巧,你在题目页面的 url 里加一个 -cn,即 https://leetcode.com/xxx 改成 https://leetcode-cn.com/xxx,这样就能切换到相应的中文版页面查看。
对于初学者,强烈建议从 Explore 菜单里最下面的 Learn 开始刷,这个专题就是专门教你学习数据结构和基本算法的,教学篇和相应的练习题结合,不要太良心。
最近 Learn 专题里新增了一些内容,我们挑数据结构相关的内容刷就行了,像 Ruby,Machine Learning 就没必要刷了。刷完 Learn 专题的基础内容,基本就有能力去 Explore 菜单的 Interview 专题刷面试题,或者去 Problem 菜单,在真正的题海里遨游了。
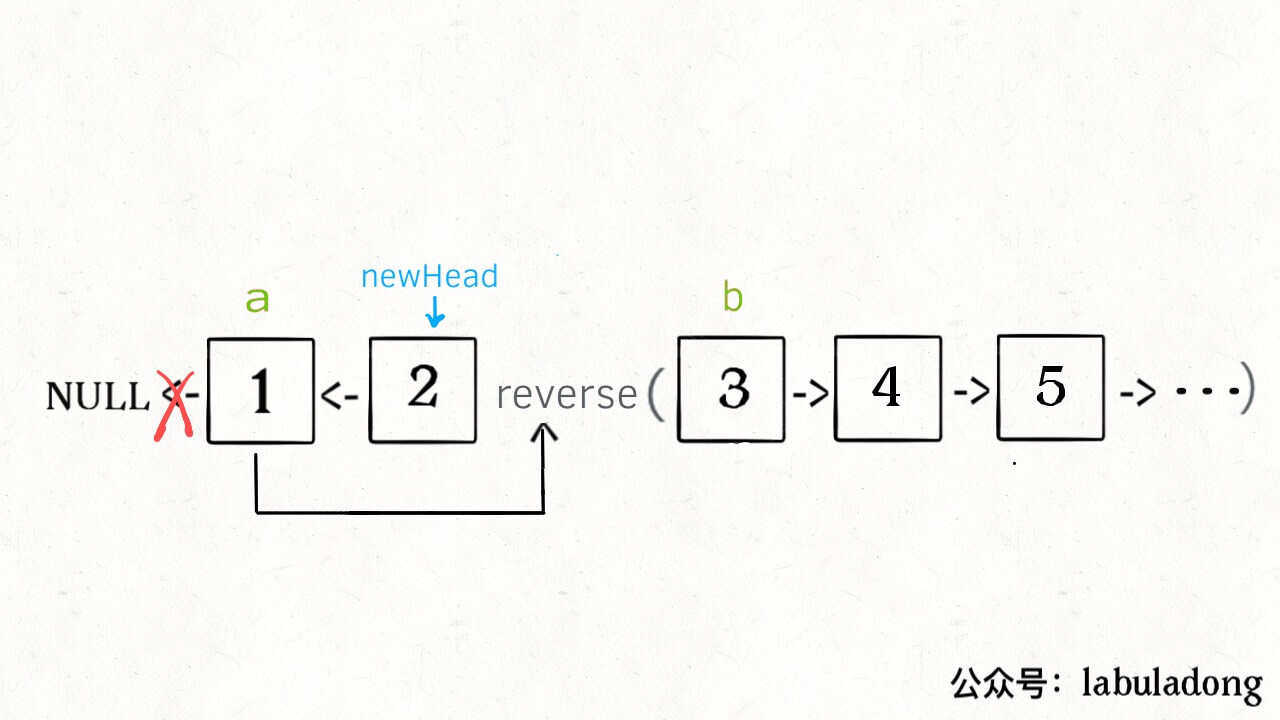
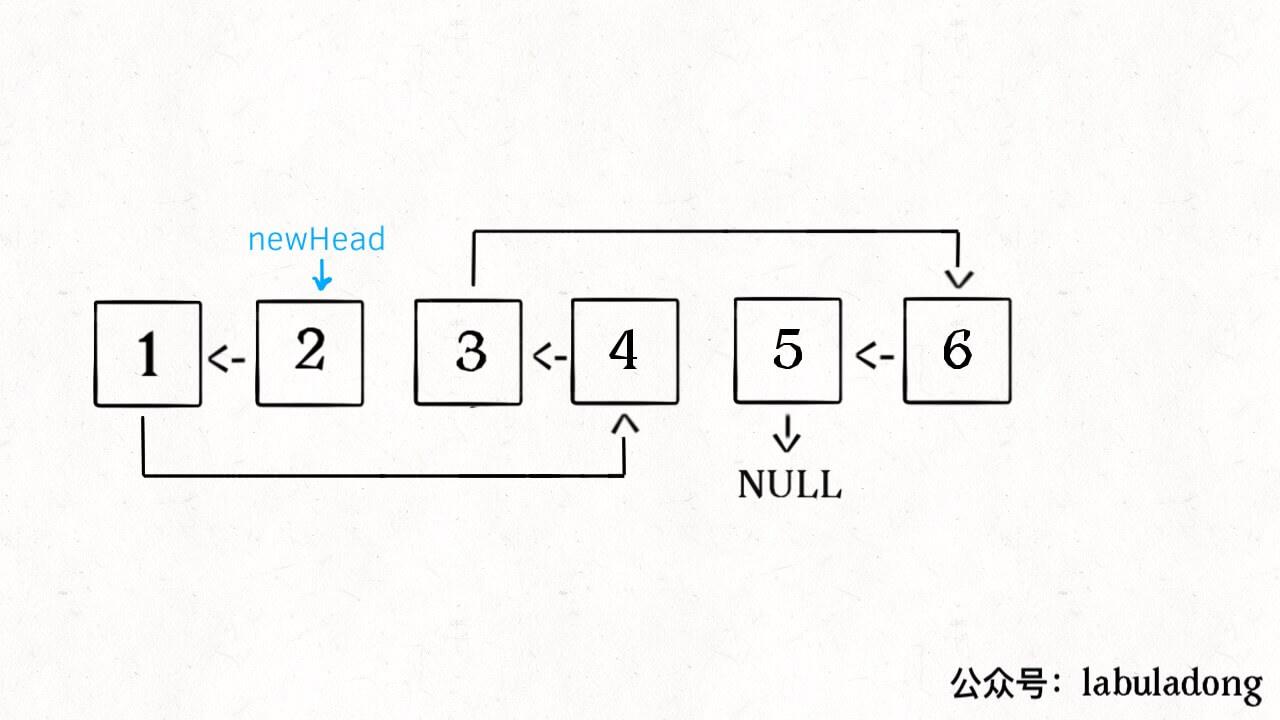
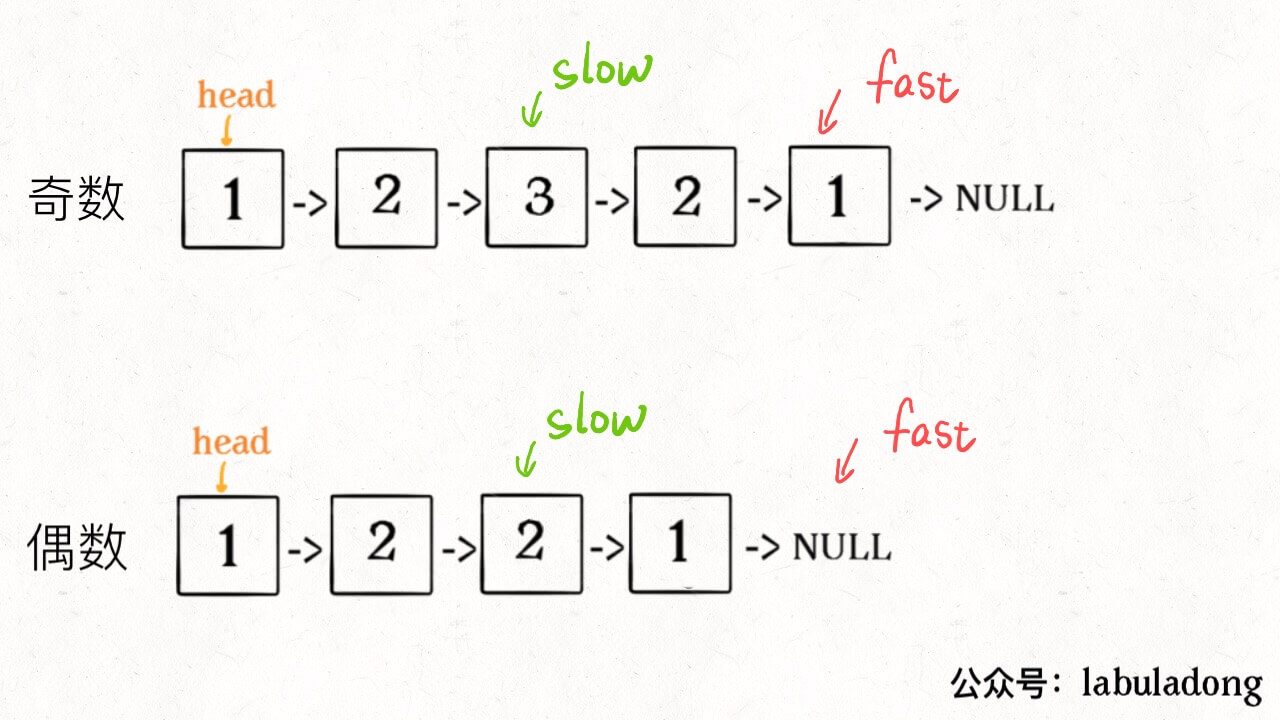
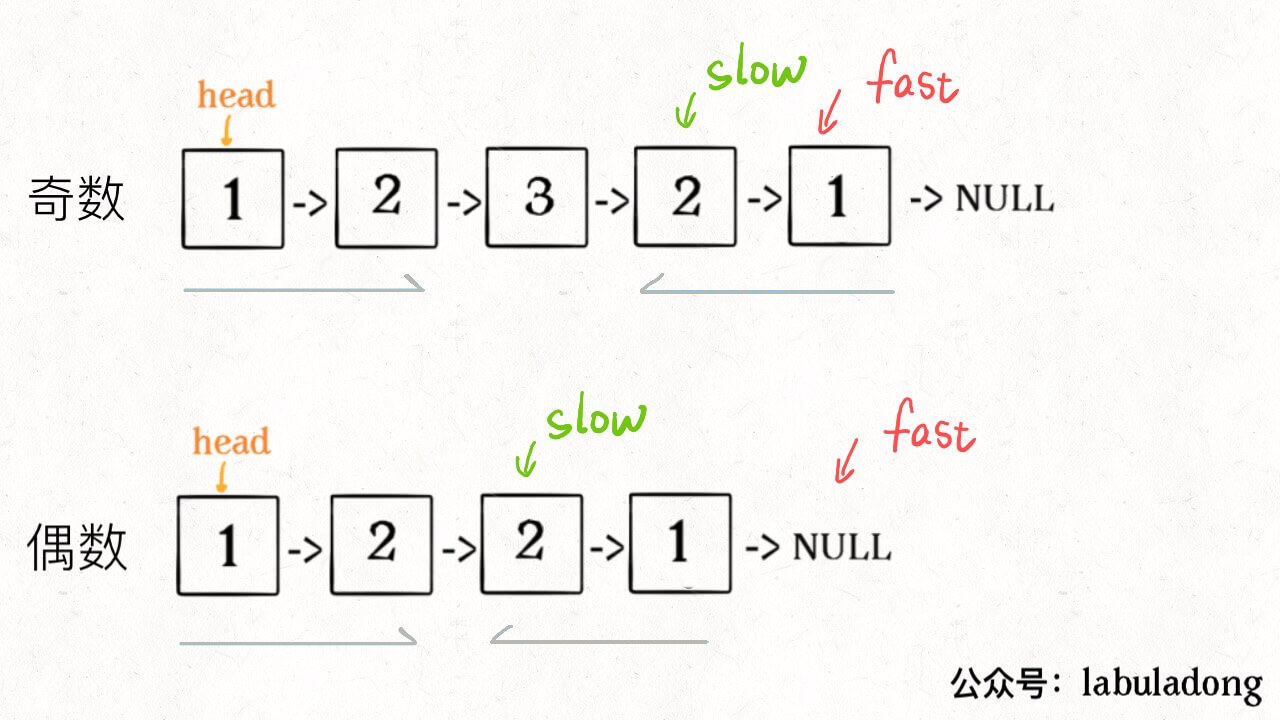
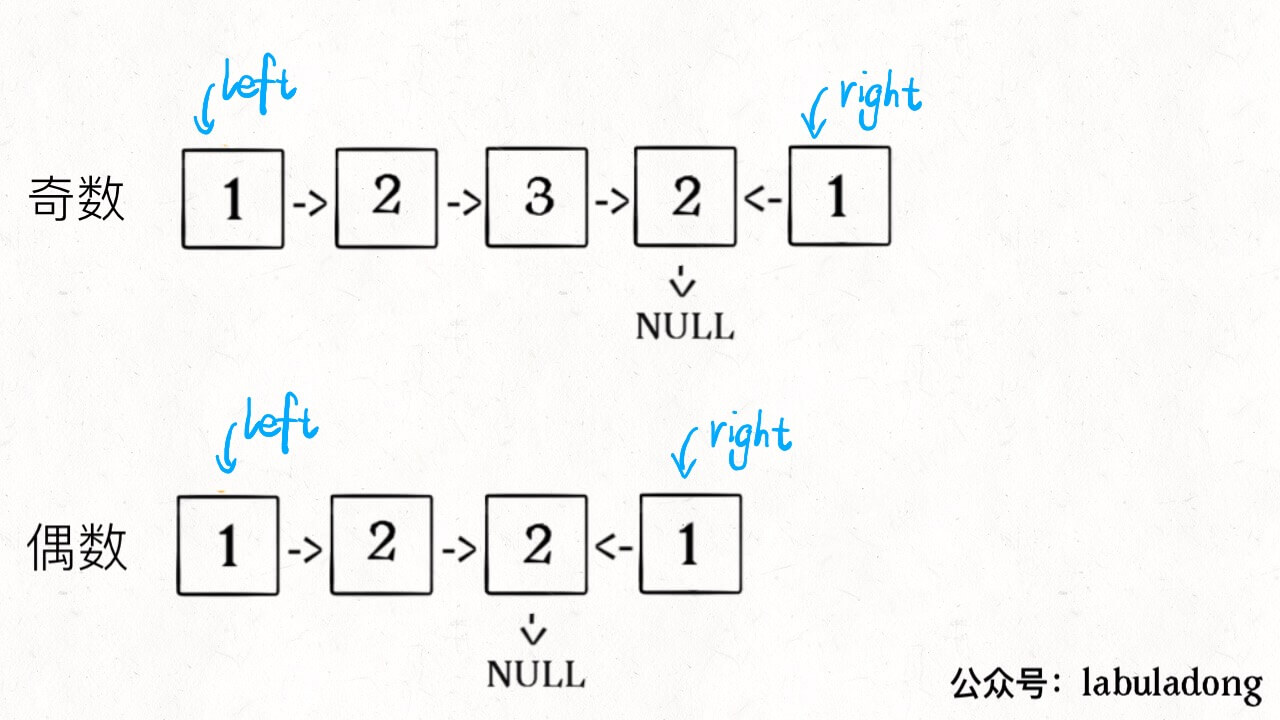
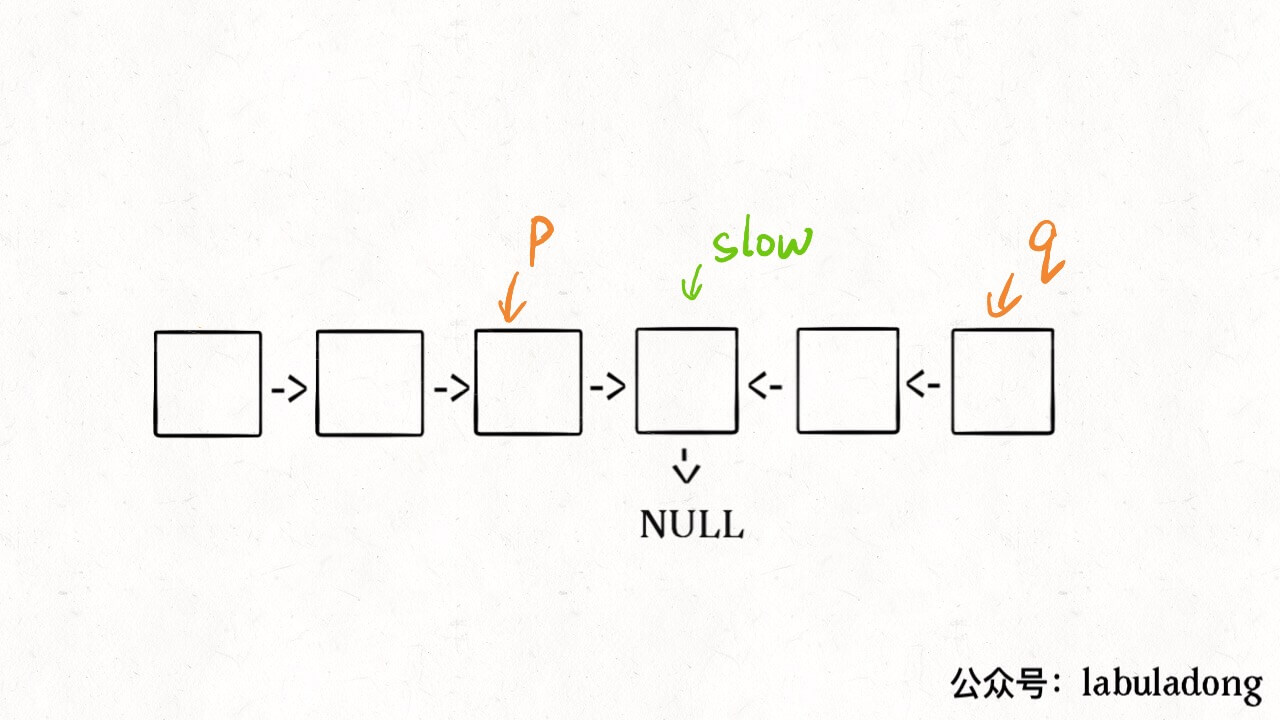
无论刷 Explore 还是 Problems 菜单,最好一个分类一个分类的刷,不要蜻蜓点水。比如说这几天就刷链表,刷完链表再去连刷几天二叉树。这样做是为了帮助你提取「框架」。一旦总结出针对一类问题的框架,解决同类问题可谓是手到擒来。
五、道理我都懂,还是不能坚持下去
这其实无关算法了,还是老生常谈的执行力的问题。不说什么破鸡汤了,我觉得解决办法就是「激起欲望」,注意我说的是欲望,而不是常说的兴趣,拿我自己说说吧。
半年前我开始刷题,目的和大部分人都一样的,就是为毕业找工作做准备。只不过,大部分人是等到临近毕业了才开始刷,而我离毕业还有一阵子。这不是炫耀我多有觉悟,而是我承认自己的极度平凡。
首先,我真的想找到一份不错的工作(谁都想吧?),我想要高薪呀!否则我在朋友面前,女神面前放下的骚话,最终都会反过来啪啪地打我的脸。我也是要恰饭,要面子,要虚荣心的嘛。赚钱,虚荣心,足以激起我的欲望了。
但是,我不擅长 deadline 突击,我理解东西真的慢,所以干脆笨鸟先飞了。智商不够,拿时间来补,我没能力两个月突击,干脆拉长战线,打他个两年游击战,我还不信耗不死算法这个强敌。事实证明,你如果认真学习一个月,就能够取得肉眼可见的进步了。
现在,我依然在坚持刷题,而且为了另外一个原因,这个公众号。我没想到自己的文字竟然能够帮助到他人,甚至能得到认可。这也是虚荣心啊,我不能让读者失望啊,我想让更多的人认可(夸)我呀!
以上,不光是坚持刷算法题吧,很多场景都适用。执行力是要靠「欲望」支撑的,我也是一凡人,只有那些看得见摸得着的东西才能使我快乐呀。读者不妨也尝试把刷题学习和自己的切身利益联系起来,这恐怕是坚持下去最简单直白的理由了。